Functional Finance and the Debt Ratio—Part I

This five part series will explore at length (warning!) and in detail (another warning—wonk alert!) the MMT perspective on the debt ratio and fiscal sustainability. While the approach suggests a macroeconomic policy mix and strategies for both fiscal and monetary policies that most neoclassical economists currently believe are unsustainable, ultimately the MMT preference for a significant role for fiscal policy in macroeconomic stabilization is shown to be consistent with traditional neoclassical views on fiscal sustainability.

This first part defines the correct measure of the national debt and then looks at the mathematics of debt service and the debt ratio.

Which measure o f the national debt is the relevant one?

Here are several measures of the national debt and the debt ratio (data as of September 2012):

Total debt ($15.86T or 102% of GDP)
Debt held by the government trust funds ($4.81T or 31% of GDP)
Debt held by Federal Reserve and private investors ($11.04T or 71% of GDP)
Debt held by private investors ($9.38T or 60% of GDP)
Debt held by the Federal Reserve ($1.66T or 11% of GDP)
Debt held by foreign investors ($5.29T or 34% of GDP)

Note that these measures are not mutually exclusive. Measures 2 and 3 are included in 1. Numbers 4 and 5 combine to equal number 3. Number 6 is included in 1, 3, and 4.

Neoclassical theory of the intertemporal budget constraint is clear on which measure is the relevant one: the appropriate measure is that part of the national debt owned by the non government sector. This would be number 4 above. Why is it the right one? Because it counts only the debt that can have direct macroeconomic implications through default on private sector held debt or through transfers to the non government sector as a result of debt service.

Note again that this is neoclassical economic theory, not MMT, and it’s already in all the graduate textbooks if you look carefully at the formulas. And because MMTers agree—at least in the sense that if one of the measures does matter, that is the one—then this means that all economists should agree that number 4 is the relevant measure of the debt ratio. If they don’t, then they don’t understand their own preferred school of macroeconomics.

So, the US debt ratio is 60%. Not 102%. Sorry, national debt clock watchers. Even by neoclassical standards, the US debt ratio is very modest, and is actually within the EMU’s Maastricht criteria. True, there might come a time that the Fed sells the Treasuries it owns through its “exit strategy” from “unconventional operations” (which on its own represents a lack of understanding of these operations—a topic for another time), but even then the debt ratio is still only about 65% or so (the Fed won’t sell all of its Treasuries as they are purchased to offset the reserve drain from increases in currency in normal times).

Debt Service vs. the Debt Ratio

Of course, the debt ratio is projected to rise, perhaps by a lot, which is the real concern of so many. But why does the debt ratio matter? Or does it? Obviously, the debt ratio itself doesn’t do anything—debt service is what ultimately will bring inflation (as the government services unbounded growth in interest obligations given that a government can always “afford” to do so merely by crediting bank accounts in its own fiat currency) or default as a result of the desire to avoid inflation. Both are obviously ruinous. So, mathematically speaking, the sustainability of the government’s fiscal position is not about the government’s ability to spend by crediting bank accounts—though this is very important for understanding (a) why a government can always “afford” policy actions that enable a full employment economy and (b) why it can never be forced into involuntary default via an inability to pay or service its debts—as much as it is about the size of the debt service relative to the size of the economy. In order to keep debt service from rising without bound relative to the productive capacity of the economy, mathematically one of two things need to happen.

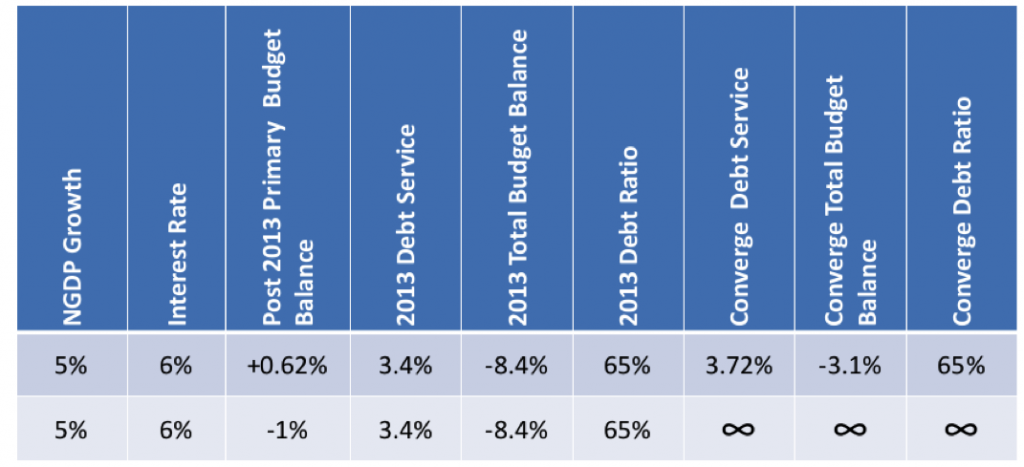
The first is that the government’s primary budget balance (that is, the budget position before adding debt service) can be sufficiently in surplus such that the government is not issuing new debt to pay all of its interest. How big the primary surplus must be depends on a number of things. For instance, if we start at the current debt ratio of 60% and assume that the primary budget balance for 2013 will be about -5% (it was 5.5% in 2012), then assume on average the rate of nominal GDP growth will be 5% and the average interest rate on the national debt will be 5%, in that case the primary budget balance after 2013 that will be required for debt service to ultimately converge (i.e., stop growing) is a surplus of 0.62% of GDP on average. This is shown in the first row of numbers in Table 1 below. This enables the debt ratio to return and converge to the 65% level that it stands at in 2013 (by assumption given the primary deficit of 5% assumed for 2013). As an aside, note that the total budget balance that is converged to is 3.1% of GDP—in other words, even in the neoclassical model—a permanent budget deficit is sustainable; while most economists (should) understand this already, the public generally does not, so it’s worth emphasizing. The second row of numbers in Table 1 tells us that even a modest primary deficit of 1% of GDP leads to unbounded growth in the debt service, total budget deficit, and debt ratios.

Table 1
2012 Debt Ratio = 60%
2013 Primary Budget Balance = -5%

Alternatively, the second thing that could happen is for the interest rate on the national debt to be low enough that a permanent primary deficit can be consistent with debt service that does not grow without bound relative to the capacity to produce goods and services. The first row of numbers in Table 2 shows that to converge at the 2013 level, the primary budget balance can be -0.62% of GDP forever if the interest rate on the national debt averages 4% rather than 6%–that is, the rate on the national debt is smaller than the growth rate of GDP. In this case, debt service is 2.48% of GDP and the primary budget balance is again -3.1% of GDP. More importantly, given an interest rate lower than GDP growth, any primary budget deficit will eventually converge—so, the second row of numbers in Table 2 shows that a primary budget balance of -1% will converge at a debt ratio of 105% and debt service of 4%.

Table 2
2012 Debt Ratio = 60%
2013 Primary Budget Balance = -5%

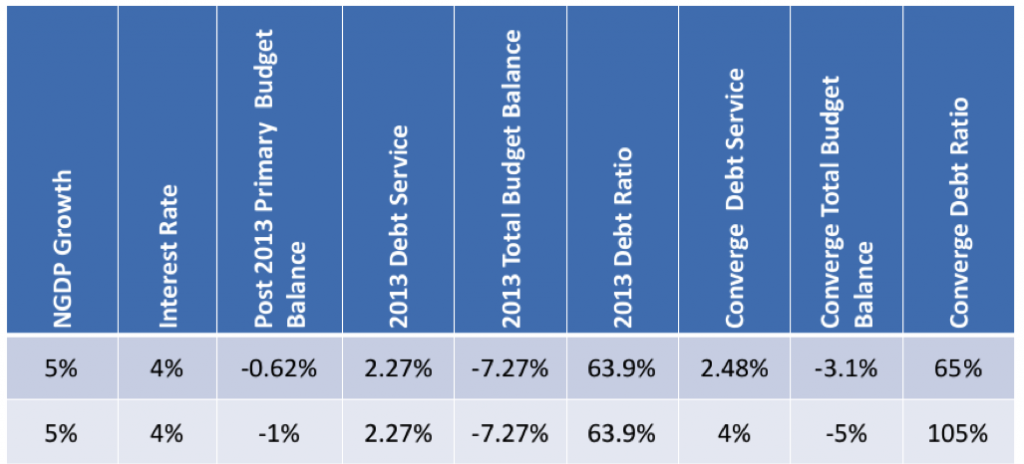
Table 3, taken from a paper I wrote in 2006, shows how different rates of interest—all less than the assumed growth rate of GDP—are consistent with convergence of debt service at a finite level of GDP for various primary deficits run into perpetuity, even fairly large ones relative to GDP. (The table also incorporates the fact that bondholders will pay taxes on a portion of the debt service.)

Table 3
from Fullwiler (2006)

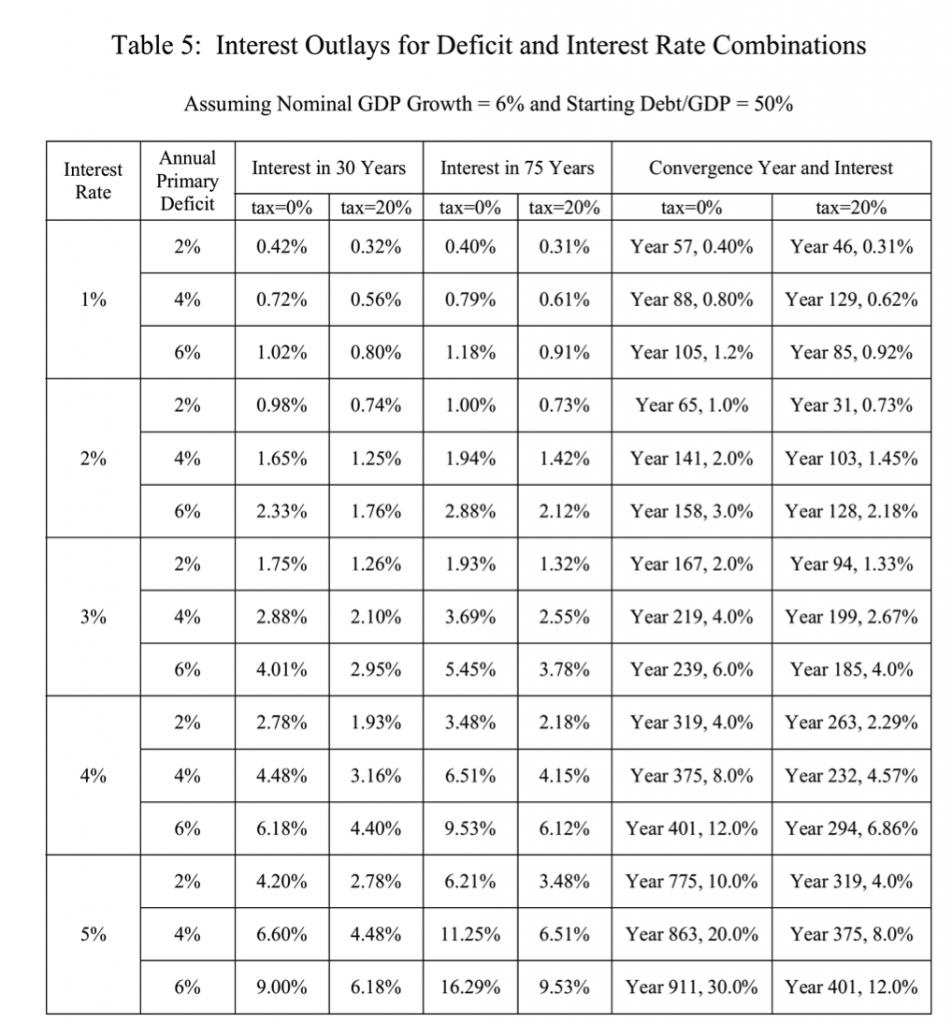
Of course it’s not necessarily the case that every one of these levels of debt service would not be inflationary—all of them could be, or none of them, depending on the state of the economy. Regardless, in terms of convergence or unbounded growth of the debt ratio, as Jamie Galbraith put it, “it’s the interest rate, stupid!” since any level of primary deficit can converge if the interest rate is below the growth rate.

Nonetheless, while MMTers like to focus on the interest rate relative to the growth rate of the economy, neoclassicals focus on the size of the primary deficit. The reason is that, as we hear every day, the bond vigilantes will attack if we don’t get our “house in order” and bring down projected primary deficits. While interest rates are low now, they say, bond markets could rebel or China could sell its Treasuries and interest rates on the debt will skyrocket. In that case, debt service will skyrocket, too, and so then—as explained above—the choice for the government will be between “printing money” to finance unbounded growth in debt service or default, which is essentially a choice between death by hanging or lethal injection. And so the fact that there are bond vigilantes can determine interest rates on US debt means the only point of focus should be on the primary deficit.

Further their actions to raise interest rates can be sudden, we are warned. As Robert Rubin, Peter Orszag, and Allen Sinai wrote in 2004 (pasted from my 2006 paper),

And here we see why the debt ratio and projected debt ratio matter to neoclassicals—they strongly influence investor confidence that itself strongly influences interest rates on government debt. This is just like when credit ratings for private companies or state/local governments are driven partly by debt ratios, which then significantly affect interest rates charged to borrowers. Mankiw and Ball (2005) summarize the feelings of the vast majority of economists, policymakers, and others—“We can only guess what level of debt will trigger a shift in investor confidence . . . If policymakers are prudent, they will not take the chance” of finding the precise tipping point that generates unbounded growth in debt service relative to the economy’s capacity. So, we are told, it is in fact about the current and projected debt ratios, which will ultimately drive debt service through the rates set by private bond markets, and the only guarantee of both mathematical and actual sustainability is to set policy such that the future shows projected futures surpluses, not deficits. In short, governments—even currency issuing ones—are at the mercy of market confidence.

In Part II, we’ll look at how interest rates on the national debt are determined.