Money and Banking Post 20: Pricing Securities

A Small Detour: Savings Account and Interest Compounding

A typical way to think about interest rates is to study how a savings account works. Suppose Mr. X puts $1000 in a savings account that provides a one percent annual interest rate. In that case, X will get at the end of:

• Year 1: $1010 = $1000(1 + 0.01)
• Year 2: $1020.1 = $1010(1 + 0.01) = $1000(1.01)²
• …
• Year 5: $1051.01 = $1000(1.01)⁵

Several things are worth noticing:

• The rate of return is fixed by the issuer of the account (1%)
• Principal rises over time: The longer X keeps the funds in his saving account, the greater, the total amount of principal due by a bank when X chooses to withdraw all its funds.
• Income rises over time: Interest income earned is automatically added to the outstanding amount of funds ($1000, $1010, etc.) so income earned changes every year as more funds are accumulated: $10 the first year, $10.1 the second year, $10.2 the third year…

Most securities work quite differently.

Back to Securities

Many securities are standardized financial contracts with the following characteristics:

• Income earned is either fixed (coupon of bonds) or unrelated (dividends) to the amount paid to acquire the security: X earns $10 every year on a bond, X earns $10 of dividend if a profit exists.
• Principal due by issuer at maturity is fixed, it is the face value (typically $1000 for bonds).

Thus, buying a security is equivalent to buying a given future stream of cash flows (income and principal). The question become to figure out how much one is willing to pay today to get access to these future cash flows? The answer is that it depends on the rate of return one wants to get. Contrary to a savings account, the rate of return can be changed according to the desires of bearers. The following sections work first with bonds and then generalize the analysis.

A Simple Rate of Return: Current Yield

At its core, the rate of return measures the reward obtained relative to the effort necessary to get that reward:

Rate of return = what you get/what you paid to get it

So in terms of securities the rate of return is:

Rate of return = monetary benefits provided by a security/price paid for a security

To simplify, one may reduce the benefits to a single coupon earned; this type of rate of return is called the current yield:

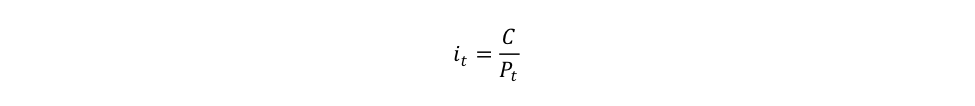
For example, if Eric wants to borrow funds from you by issuing a bond with a face value of $1000 that pays an annual 1% coupon rate for 5 years—a 1% 5-year bond—it means that:

• Each year Eric pays you a coupon worth $10 (= coupon rate*face value = 0.01*$1000)
• At the end of the fifth year, Eric gives you $1000.

The question is: are you willing to give Eric $1000 for the bond?

• If yes, it is means that a 1% reward is high enough for you: you paid $1000 to get $10
• If no, how could you raise the reward without changing the term of the bond (coupon rate, term to maturity, face value cannot be changed)? Answer: Give less dollars for the bond. If you wish to have a:
  • 4% rate of return, you should pay $250 for the bond to receive $10 every year: $10/$250 = 4%.
  • 5% rate of return, you should pay $200
  • 10% rate of return, you should pay $100

As you may note, the less you pay the higher the rate of return. The price P paid for the bond at any given time is positively related to a fixed coupon C, and inversely related to the desired rate of return i that prevails at any given time:

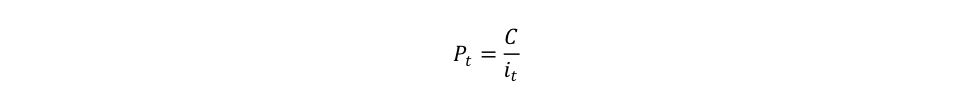
This inverse relationship between the price of a bond and its rate of return holds in cases that are more complicated and is an important point to remember.

Adding One Complication: Time

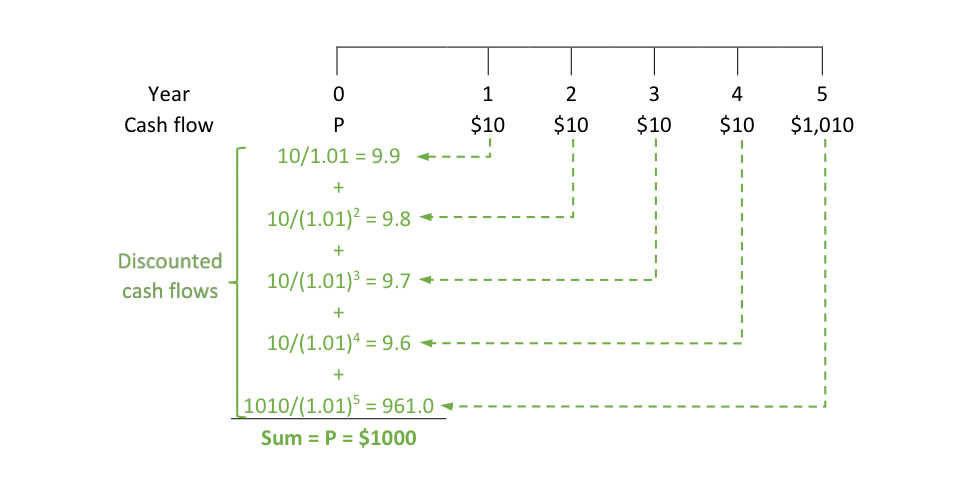
The previous section studies the pricing of securities from the point of view of one income. There may be several fixed coupons that are paid over time and the principal is paid at maturity. Going back to Eric’s bond the stream of cash flow is:

What should you pay for that stream of cash flows? Again, the answer depends on the rate of return you want for each cash flow. Say you are fine with a 1% rate of return, then to get that rate of return on the cash flow of:

• Year 1, you must pay today approximately $9.9 because $9.9 placed over one year at 1% gives $10: $9.9(1.01) = $10.
• Year 2, you must pay today approximately $9.8 because $9.8 placed over two years at 1% gives $10: $9.8(1.01)² = $10.
• …
• Year 5, you must pay today $960.98 because $960.98 placed over five years at 1% gives $1010: $951.57(1.01)⁵ = $1010

One may note that, in order to find the proper amount to pay today for a specific future cash flow, one must work backward with the rate of return desired. Indeed, given that the future cash flows are known, the point becomes to figure out what each of these flows are worth today given the desired rate of return. This is called discounting cash flows, and the discount rate is the desired rate of return. The sum of all the discounted cash flows until maturity is called the present value, or fair price, of Eric’s bond.

This is the price that you ought to pay, if a 1% rate of return is satisfactory and you plan to hold the bond until maturity. Note that, for a desired rate of return of 1%, the fair price equals the face value of the bond. This is consistent with what was found with in the section about the current yield. Of course, if you desire a higher rate of return, you will want to pay less for the bond. For example, if you desire a rate of return of 5%, you should pay $826.82 (just replace 1.01 by 1.05 in the previous sum).

The rate of return obtained by holding a bond to maturity is called the yield to maturity. Put in mathematical form one has:

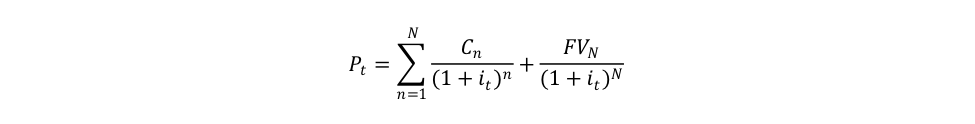
With P the fair price, C the coupon received at time n, N the term to maturity, FV the face value, and i the yield to maturity. Once again, one may note that a higher interest rate (yield to maturity) leads to a lower fair price. This can be seen even more clearly for consols or perpetuities, which are irredeemable bonds (term to maturity is infinite: N tends toward infinity) that pay a fixed coupon. In that case the fair price of a consol is:

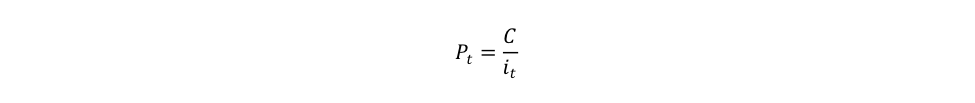
This is similar to what the previous section concluded by using the current yield.

The yield to maturity can be approximated by calculating the total rate of return, that is, the rate of return that accounts for all the incomes earned, for interest incomes earned on incomes (reinvestment income), and for capital gains/losses. Using the logic presented in savings accounts, if someone puts $1000 in a savings account and got $1050 after 5 years, one gets:

$1050 = $1000(1 + i)⁵

Solving for i we get:

i = (1050/1000)^1/5 – 1 ≈ 1%

Similarly, if a bearer paid $827 to get $1050 after 5 years the rate of return is:

i = (1050/827)^1/5 – 1 ≈ 5%

More generally the total rate of return for n years of placement can be calculated as follows:

Adding Yet another Complication: Capital Gains or Losses

The previous section assumed that someone decided to hold Eric’s bond until maturity, but what if someone does not plan to do so? What should a bearer pay Eric at issuance to get the bond? Once again, it is all about calculating a fair price by using the discounted value of cash flows. The first step is to figure out what those future cash flows are. Let us assume a bearer plans to hold Eric’s bond for only three years. He will earn three coupons and then sell the bond at the end of year 3, so the bearer studies the following stream of cash flows:

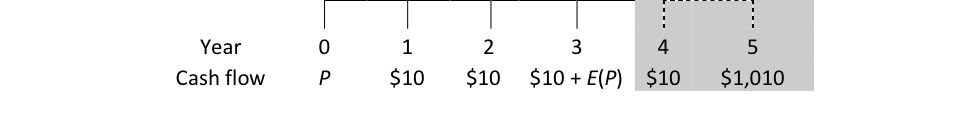
There is a new element that enters in the cash flow stream, the expected resale price E(P). The bearer is not interested in earning the last two cash flows, although, as shown in a moment, she must care about them to calculate what she ought to pay for the bond.

Given that E(P) is part of the cash flow stream the bearer must now formulate a precise expectation to calculate the fair price. One may wonder how the bearer can formulate this expectation. Should she just make up something, or is there a more systematic way to formulate an expectation? As you may have guessed the second answer is correct.

At any time the market price of a bond follows its fair price and the fair price is the discounted value of future cash flows. At the end of year 3, Eric’s bond will be a two-year bond with two cash flows left to be paid—$10 and $1010—so the expected resale price should account for these known elements. The problem becomes to discount these two cash flows. The bearer should use what she currently (year 0) expects other market participants will desire in terms of rate of return in year 3, E₀(i₃):

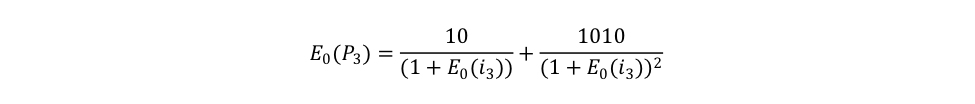
Thus, the current expectation of the bearer regarding the resale price in three years (E₀(P₃)) crucially must depend on her current expectation about the interest rate demanded on Eric’s bond by other market participants in three years. How can the bearer know what this interest rate will be? She cannot—and she knows her expectation will most probably turn out to be wrong to some degrees and she hopes not to be completely wrong. However, to make an informed decision regarding what price she is willing to pay for the bond, she must make a guess by using her intuition, some economic analysis, and/or other methods. The following section shows a real world example.

Once a bearer is armed with the cash flow stream, the only thing left to do is to compute the discounted value using her desired rate of return. So if the bearer wants a 1% rate of return over three years and expects that market participant will want a rate of return of 5% in three years on Eric’s bond, the bearer makes following calculation:

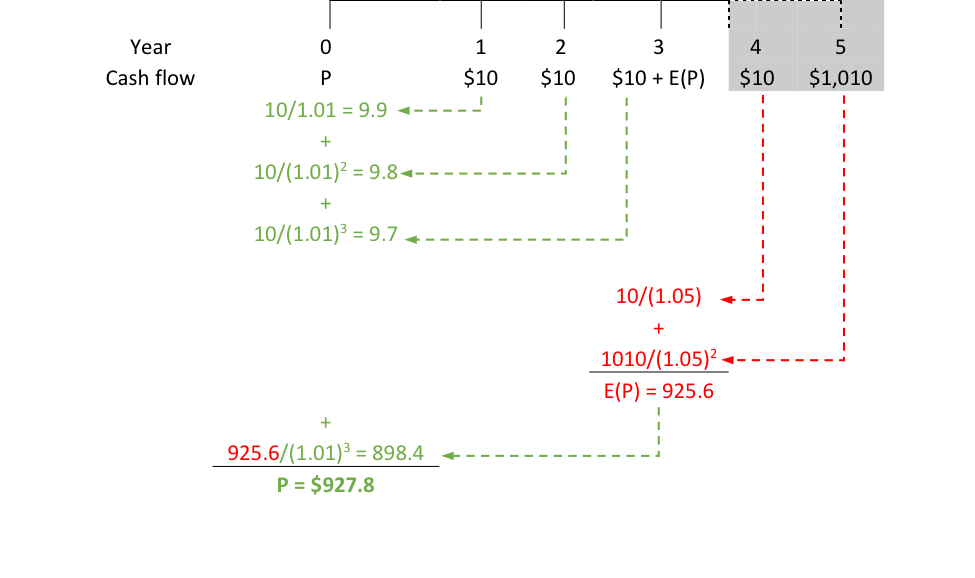
At issuance, the bearer should offer to pay $927.8 for Eric’s bond given her expectation about the resale price and so her expectation about the future interest rate on Eric’s bond. This provides the bearer an expected rate of return of 1% over three years. She will get $30 of coupons plus the expected $925.6 by the end of year 3, and will have paid $927.8 to receive that these cash flows: (955.6/927.8)^1/3 – 1 ≈ 1%.

As noted earlier, expectations rarely turn out to be correct. While the trend might have been guessed correctly, one rarely gets to make an accurate prediction of the timing or the actual value of a variable. The bearer assumed that interest rate on Eric’s bond would rise from 1% to 5%. What if at the end of year 3:

• The interest rate went up but only to 3%? In that case, the resale price of the bond is higher than expected ($990) and the total rate of return is higher than expected.
• The interest rate went up more than expected, say 10%? In that case, the resale price is lower than expected ($926.44) and so the total rate of return does not reach the desired 1%.
• The interest rate went down to 1%? In that case, the bond can be sold for $1000 instead of the expected $925. Total rate of return is much improved.

A Real World Application: QE, Deficit and Rate on Treasuries

As explained in the previous section, unless one plans to hold a security until maturity, one must make some expectations about the price at which a bond can be sold. The Great Recession led to large injections of reserves (see Post 3) and to the rise of the fiscal deficit to historical highs for the post-WWII period. A common view among bond-market participants and others was that these monetary and fiscal policy trends would generate a rise in the interest rate on Treasuries. The economic logic was based on the money multiplier (see Appendix to Post 10), the quantity theory of money (see Post 11) and the crowding out effect (see Post 12), which led market participants to conclude that inflation risk and fiscal risk had risen and so interest rates on treasuries would rise in the future. This means that they expected bond price to fall.

Armed with this logic and a set of expectations some decided anticipate the rise in Treasuries rate. They did so by implementing a portfolio strategy that involved selling their treasuries, to avoid capital losses, and/or taking a short position (see Post 19) on Treasuries, to profit from the expected fall in the price of Treasuries. Unfortunately for them, interest rates on Treasuries fell overall afterward and inflation never materialized. They forgo capital gains (if they sold their Treasuries) or recorded potential capital losses (if they took a short-position on Treasuries). As explained in Post 4, Post 6, Post 10 and Post 11 and Post 13, their economic argumentation was unsound. Not only are inflation and interest rate only loosely related, but also nominal interest rates on Treasuries are largely driven by the monetary policy stand not by the fiscal stand. As explained below, however, one must be careful to think that a sound economic argumentation can always provide a winning portfolio strategy because many other factors influence what goes on in financial markets.

Conclusion

There are two direct ways to obtain a reward from taking a position in a security. First, financial instruments embodies a promise to make future monetary payments in terms of income and repayment of the principal. Second, one may also be able to make a capital gain by reselling the security before it matures. Thus, before someone decides if taking a position in a security is worthwhile, one may ask several questions such as:

• Will the issuer be able and willing to fulfill his promise? One may want to carefully judge the creditworthiness of the issuer, especially if one plans to buy and hold the security for a long time so that income payments are the main reward.
• Will it be possible to make a capital gain? How big will it be? One may be more interested in speculating, that is, to bet about the direction of the price of a marketable financial instrument in order to make a capital gain. As explained in Post 19 that can be done by taking a short position (if one bets that price will fall) or a long position (if ones expect that price will rise).
• How long am I willing to hold a given financial instrument (either to speculate or to hold)?
• What is the rate of return on asset that I want to get? As noted above this is a crucial question and as explained in Post 7, this question can be combined with a decision about the proper amount of leverage to use to get a desired rate of return on equity.

By answering some or all these questions, one can determine at what price a financial instrument should be bought. The general formula for the fair price of a financial instrument is:

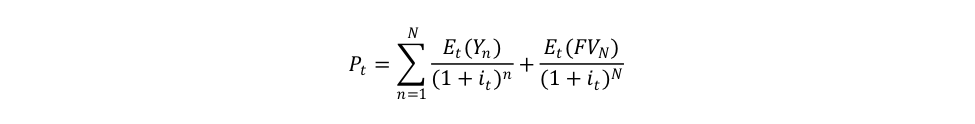
Where the subscript t indicates the present time, P_t is the current fair price, Y_n is the nominal income promised at a future time n, FV_N is the face value that will prevail at maturity, E_t indicates current expectations about income and face value, i_t is the current discount rate imposed by bearers, N is the time lapse until maturity (n = 0 is the issuance time). There is a wide variety of financial instruments that uses this formula. At one extreme are modern government monetary instruments that provide no income (Y = 0), have a zero term to maturity (N = 0, they can be redeemed instantaneously), and are universally expected to be taken back by the government at their initial face value at any time, P_t = FV₀ (see Post 15). At the other extreme are consols that pay a given coupon and have an infinite term to maturity, P_t = C/i_t. At the other extreme are also stocks. Assuming that a stock pays an initial dividend D₀ that grows over time at a given rate g, the fair price of the stock is:

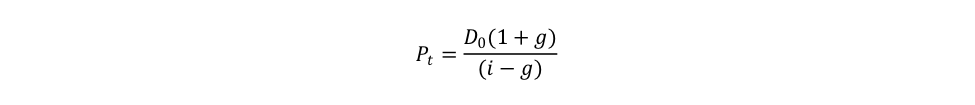
If a collateral exists, in case of default, the fair value will be depend on the expected ability of the creditors to recover some of the unpaid dues embedded in a promise. Thus, in case of default, the maximum fair value is equal to the expected value of the collateral and available recourse.

Note that the fair price is only the price at which a financial instrument ought to trade, it is not necessarily the price at which a financial instrument will trade—the market price. A discrepancy between the market price and the fair price can emerge because of the financial infrastructure in place to trade securities is not well developed, or, for example, because market participants do not have all the information needed to make an informed decision. A discrepancy may also exists because of the simplifying assumptions made to get a neat mathematical expression of the fair price. For example, the previous formula for the fair price of stocks assumed that the growth rate of dividends is forever constant. Finally, a discrepancy will exist because what is fair to pay depends on the holding period, and not all market participants have the same holding period.

The central point that this formula brings forward is that expectations about the future are central to determine what financial market participants are willing to pay for a security. If speculative behaviors dominates, E(P) is what financial market participants focus on to determine P: guess the future mood and view of market participants. If an entrepreneur approach to portfolio choice dominates, E(Y) is the main focus of market participants: buy-and-hold strategy to earn income over long run.

The i, E(Y), E(P) are impacted by credit risk, liquidity risk, solvency risk, inflation risk, tax risk, recession risk, monetary-policy risk, and many other risks—real or imagined—perceived by market participants. As such, P can fluctuate widely and changes frequently as views about i, E(Y), and E(P) change constantly. In markets where traders are very active, P will fluctuate with the mood of the time, technical problems (if automated trading is dominant), and many other non-economic reasons including the proportion of speculators and the proportion of income-seeking participants.

What this suggests is that it is pretty much impossible to predict P (and so i) on a specific security. While one may use sound economic and financial arguments to make a prediction, most market participants may not agree with that argument, or may have a different argument that involves an opposite prediction. In that case, P will tend to be influenced by the dominant view, which may not be the correct view (in terms of intellectual soundness). While financial market participants who used a sound economic and financial logic to make their portfolio choice will usually end up being vindicated, it may take years for that to happen if they are not the dominant view in a market. As the saying goes, the market can stay irrational longer than one can stay liquid and solvent.

As such, some market participants may not be interested in brainstorming about fair prices, and may prefer to use pattern recognition to try to determine if they should buy, hold, or sell a financial instrument. The chartist approach is such view. Followers of this approach study charts of past price behaviors to determine how the price will behave in the future. Certain patterns are supposed to be clear predictor of an upcoming sharp rise (or fall) in the price; one just needs to recognize the pattern in time. In the end, financial market participants use all sort of strategies and methods to implement their portfolio strategies, and they also have all sort of opinion about the different risks at play.

What if there is no Coupon? Zero-Coupon Securities

Some securities, such as T-bills or commercial papers, do not pay any coupon. In that case the valuation of the fair price is done purely with the discounted face value of the security:

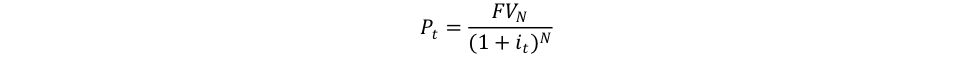
As long as interest rates is positive, the fair price will be below the face value. The fair price converges toward the face value as the term to maturity gets closer to zero. Bearers are rewarded by making a capital gain that is bigger the closer to issuance they buy the security.

Discount, Par, Premium and Arbitrage between Securities

The face value is the price at which the issuer will take back its financial instrument when it matures. It is usually inscribed on the face of the financial instrument but not always as explain in Post 15. The market price of a security—the price at which it circulates among bearers—is usually different from the face value. If, to simplify, one assume that the fair price and market price are the same, then three situations as possible:

• If P > FV: A security trades “at a premium.”
• If P = FV: A security trades “at par” or “at parity.”
• If P < FV: A security trades “at a discount.”

One may wonder why a security would sell at a premium. That is, why would someone be willing to pay more today than the principal that will be received at maturity? Someone may pay $1200 for a bond with a face value of $1000. One reason is that coupon rate on the bond is higher than current interest rate (which is the currently desired rate of return), so market participants are willing to pay more for the bond. As explained in Post 5, another reason is that someone intervenes to ensure that capital gains can be made by others, and is willing to record capital losses at maturity.

For example, let us assume that all bonds have a face value of $1000 and all bonds carry the same credit risk. In January 2017, Corporation X issues 10% 5-year bonds, that is the coupon rate is 10% (and so the coupon is $100) and the term to maturity is 5 years. At that time, the interest rate on bonds is also 10% so X is be able to sell its bonds at par ($1000) and bearers get a 10% rate of return, just what they desired. After January 2017, the corporate bond rate falls to reach 5% by January 2018, so corporations now issue bonds that pay a lower coupon rate (say 5% and so $50 of coupon). While the desired rate of return has fallen, the coupon rate on the bonds issued by X in 2017 is still 10%. As such there is a high demand for them, which raises their price. The question becomes to figure out by how much the price will rise.

The general answer is that the price will rise until financial market participants are indifferent between buying the 10% bond and a 5% bond. Remember that the rate of return is what you get for what you paid. So a quick dirty answer to the question can be provided by using the current yield: the price of the 10% bond will have to rise to $2000 because getting $100 for $2000 is equivalent to getting $50 for $1000. This is, of course, a simplification because one needs to calculate the fair price to get a full answer that accounts for time. In January 2018, the bond issued by X in January 2017 is now a four-year bond, which means that its fair price, if held to maturity, is:

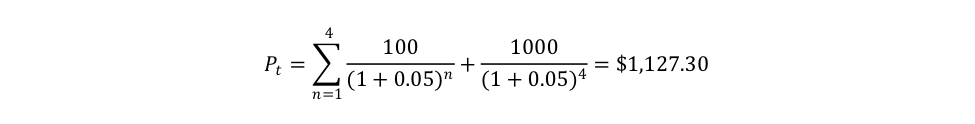
The January 2017 10% bond issued by X sells for $1127 in January 2018. This provides of rate of return (as calculated by the yield to maturity) of 5%.

The act of buying and selling securities in order to equalize rate of return is called “arbitraging.” Arbitrage is an important portfolio strategy for market participants who are always on a look out for securities with a price that is inconsistent with the desired rate of return of the moment. With computers, this kind of activities involved millisecond price deviations and thousands of trades in the blink of an eye.

Bubbles or Not: Are Financial Market Efficient?

One question that has kept some economists busy for a few decades is whether financial markets are efficient. The Bank of Sweden recently decided to aware its price to economists with very different views on the question: Eugene Fama (who argues that they are) and Robert Shiller (who argues they are not). This question is especially important for economists who work in the framework of a real exchange economy that sees markets as the central mechanism to allocate correctly scarce resources (see Post 12). If market are efficient, they are able to collect all the relevant information to price securities, and so market participants are able to make informed portfolio decisions. In the process funds are transferred from savers to investors and economic activities that are the most efficient (that is the ones are able to produce a given amount of output with the least amount of inputs) receive funds. Non-efficient economic activities do not receive funds and are weeded out by market processes.

The efficient market hypothesis (EMH) comes in different forms. The strong form argues that all private (confidential information that only the managers of a firm know) and public information are included in the pricing mechanism. The semi-strong hypothesis argues that only publicly available information is included. The weak form focuses on a subset of publicly available information—namely past prices of securities—and argues that markets are efficient if the prices of securities cannot be predicted in the short-run by using past prices. Prices of securities move in a random fashion as information arrives randomly. Fama argues that evidence for the weak and semi-strong hypotheses are mostly favorable. Shiller argues that this is not the case.

An implication of the efficient market hypothesis is that the price of a security cannot deviate at all (for the strong hypothesis) or for a long time (for the weak hypothesis) from its fundamental value. Another implication is that it is impossible to predict the price of securities by using past prices because past and future prices are independent from each other. This is quite the opposite conclusion to the chartist approach who sees all sort of patterns in past prices that indicate future past trend.

The fundamental value is the one that reflects all the relevant information necessary to price a security—dividends for stocks, coupons for bonds. Even capital gain expectations are only a reflection of future income payments, so one can assume that the fair price is just a discounted sum of future incomes, and the fundamental value V is:

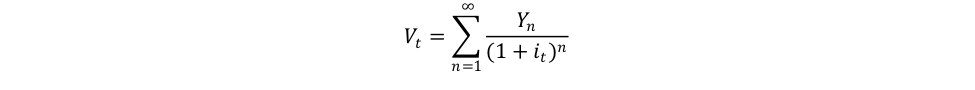
There is, however, a deeper reason why this is called the fundamental value. The incomes (Y) are supposed driven by what economists of the real exchange economy framework see as fundamental economic forces, technology, time preference, and the amount and allocation of resources. Market prices reflect the “true” supply-side economic conditions of an economy, and so provide a clear means to allocate scarce resources. Markets allocate correctly resources as long as market prices equal their fundamental value.

This fundamental value is supposed to be a strong attractor for the fair price (P moves toward V). While bubbles—deviation of the fair price from the fundamental value—are possible at least in the weak form of the EMH, they do not last and are marginal. Markets tend to self-correct quickly because of arbitrages by speculators. Speculators are a stabilizing force as Friedman (1953: 175) argued: “People who argue that speculation is generally destabilizing seldom realize that this is largely equivalent to saying that speculators lose money, since speculation can be destabilizing in general only if speculators on the average sell when the [security] is low in price and buy when it is high”. Speculation corrects price misalignments because well-informed speculators are supposed to be rational agents who act upon the information available to calculate the fundamental value of an asset. If P > V speculators expect that the price will go back to its fundamental value; therefore, they anticipate capital losses by selling the assets for which this is the case. This decreases the market price and brings it back to its fundamental value. Inversely, when P < V, speculators anticipate capital gains by buying the assets concerned, which increases P and brings it back to V. Thus, well-informed speculators complement market participants seeking to keep securities in their portfolio, which help to speed up the adjustment process in imperfect markets. Speculators that do not act on that basis are eliminated by market mechanism as they record loses.

As discussed in Post 12, quite a few economists have disagreed, not only with the characterization of economics as the science of allocation of scarce resources, but also with the view of an economy driven by supply-side factors that are supposed to be independent from demand factors. The fundamental value is not a strong anchor and can be influenced by current price conditions (V moves toward P). They have also disagreed with the role that this view gives to financial markets and how participants operate in that market.

John Maynard Keynes, who was an economist and a financial manager, among other things, summarized his own view on the topic by using the analogy of a beauty contest. In a traditional beauty contest, each judge is asked to select the most beautiful woman according to his/her own opinion. This is equivalent to financial market participants trying to pick the securities based on fundamentals. One must evaluate carefully the creditworthiness of an issuer by working though accounting documents, by getting a grasp of the competence and character of the managers (perhaps by meeting them or by reading about them), by understanding the business model and potential competitors, among others. Then, one needs to wait patiently for years to earn accumulate some incomes. Put differently, buying and holding securities for the long run makes someone equivalent to an entrepreneur, because the financial success of that person depends on the success of the business.

Keynes argues that most financial market participants do not behave that way when they make portfolio choices (although Keynes himself apparently did follow that type of decision-making process). Most people do not want, or do not have the time and knowledge, to do that. There are three reasons for this. First is human nature, second is competition, and third is the existence of liquidity. In terms of human nature, not only is it tedious and time consuming to evaluate the creditworthiness of issuers, but also most humans are driven by the thrill of speculation and the quick results that gambling can provide. These quick results, if positive and large, may create envy and remorse from those who preferred to wait patiently, and may drive them to change strategy and become speculators rather than entrepreneurs.

Second, competition is strong among financial market participants, those that record the highest short-term rate of return will gain clients, while those that are behind will lose clients. If speculative behaviors provide the highest short-term rate of return, as they tend to do in good times, financial market participants will adopt them. Portfolio managers (pension funds, mutual funds, etc.) do see large movement of funds in an out of their firm depending on quarterly results, even if their placement strategy is based on long-term results. Warren Buffet provides another example of the pressure of competition and search for quick results. In the late 1990s, the price of the dot.com stocks (Amazon, etc.) was growing very rapidly allowing holders to make huge capital gains. Mr. Buffet refused to buy stocks of dot.com companies on the ground that they were not making any profit and the business model was not well established. The share of his business conglomerate, Berkshire Hathaway, fell during that period as shareholders left to find portfolio managers that would but place funds in dot.com companies. Mr. Buffet did not mind, his business has the financial strength to sustain short-term swings in financial moods, and the dot.com bubble burst proved him right; but he had to forego massive potential capital gains during the boom years, which most market participants are unwilling or unable to ignore.

Finally, beyond human nature and competition, it is risky to follow an entrepreneur-like portfolio strategy. The liquidity of securities helps lessen that entrepreneurial risk (one can sell quickly if not satisfied with the performance of securities), but the existence of that liquidity ends up influencing portfolio choices. One way is because the more liquid a market is, the more speculative behaviors are promoted because it is easier to make quick capital gains. Another is because of the uncertainty of the future and the liquidity risk that exists from holding securities. For example, one may be willing to wait patiently but suddenly may need to sell securities to meet unexpected expenses. If, at that time, prices of securities are very low (for reasons that may or may not be related to the performance of their issuers), it may be difficult if not impossible to meet expenses and one may become insolvent. Thus, individuals must account for expected short-term price direction even if they do not make portfolio decisions mostly based on that criterion. They do so because, unlike Warren Buffet, they usually do not have the financial means to wait for the price to go back up; their savings is too small so they must sell at a loss.

Thus, for all these reasons, Keynes notes that financial markets do not behave like a traditional beauty contests, and it is rational for them not to behave that way. In Keynes’s beauty contest—which encapsulates his view about how financial market participants behave—each judge is asked to figure out what the average opinion of the other judges is about the most beautiful woman. This is quite similar to the chartist approach that wants to predict future prices (and so future average opinion) out of past prices. Keynes notes that some market participants may even be concerned with guessing what the average opinion thinks the future average opinion will be, and so on. It is quite a self-referential behavior, far removed from the painstaking and cold analysis of the issuer’s creditworthiness. Thus, speculation is a destabilizing force that is not eliminated by market mechanisms, but rather promoted by them. Keynes concluded: “Speculators may do no harm as bubbles on a steady stream of enterprise. But the position is serious when enterprise becomes the bubble on a whirlpool of speculation. When the capital development of a country becomes a by-product of the activities of a casino, the job is likely to be ill-done” (Keynes 1936, 159). Activities in financial markets may become only remotely related to what goes on in terms of economic activity (production, consumption, investment), and financial markets may become a giant gambling machine. The financialization of the economy further reinforces this disconnection and Post 18 showed that the stock market in the United States is not a net provider of funds to businesses.

TO GO FURTHER: DURATION AND CONVEXITY

This chapter explains what the price level of a security ought to be and what influences that price level. While this is a central concern of financial market participants, an equal concern is to figure out how sensitive the price of a security is to changes in interest rates. The Post shows that if the desired rate of return of market participant changes, there is some implications for the pricing of securities and some of them may end up trading at a premium, while other may end up trading at a bigger discount. Market participants who want to hold securities and those looking to make capital gains want to get an idea of how much the price will change.

More broadly, financial institutions are interested in knowing how the net worth of their balance sheet will change if interest rates change because securities on the asset and liability side of their balance sheet may be marked to market. For example, if interest rates go up the market price of securities will fall and so the value of assets and liabilities will fall. Depending on how sensitive the value of securities held (assets) is compared to the value of securities issued (liabilities), net worth may go up, down or stay unchanged.

To calculation this sensitivity, one needs the duration on a bond. Start with the fair price formula:

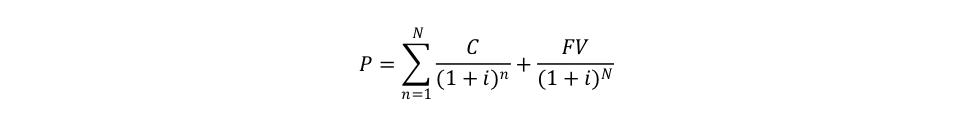
Taking the first derivative, we have:

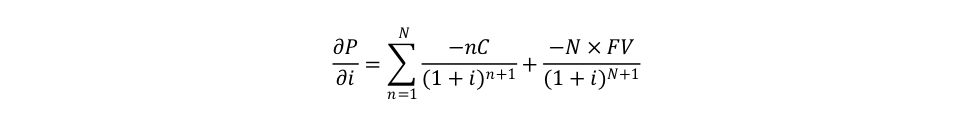
By factorizing by 1/(1 + i) we have:

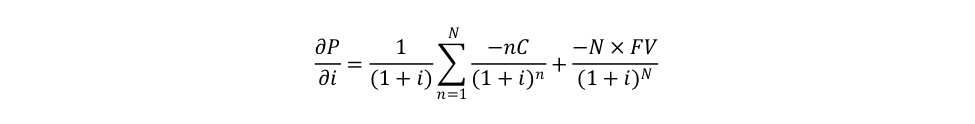
The (Macaulay) duration DUR is the ratio of the time weighted discounted cash flow and the discounted cash flow:

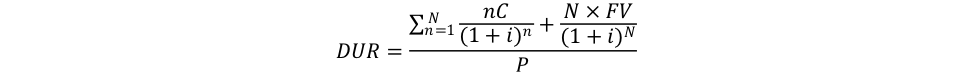
The ratio measures a number of years. One may note that for zero-coupon bond (C = 0), the duration is the term to maturity (N).

Taking the formula of duration and substituting in the first-order derivative, it follows that:

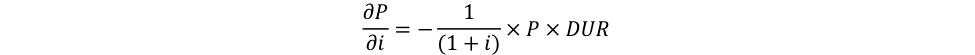
Alternatively:

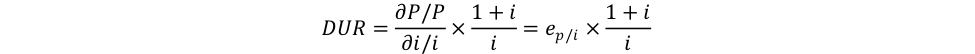
Thus, the duration reflects the elasticity of price to interest rate.

If one wants to know by how much percentage wise the price of a security changes following a change in the interest, someone calculates:

 is called the modified duration and is used to measure percentage changes in the price following a one percentage point (100 basis points) change in the interest rate (∆i = 0.01).

If someone wants to know approximately by how much the price level of a security changes following a change in the interest rate, one calculates:

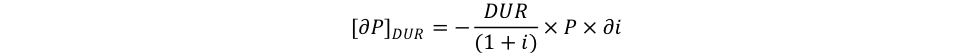
is called the dollar duration, it measures the absolute changes in the price following a 1 percentage point change in the interest rate. It is the product of the modified duration and the price level of the bond.

For example if the 1% 5-year bond is currently trading at parity and the interest rate rises by 50 basis points, then one can calculate the approximate impact on the price of the bond as follows:

• Interest rate went from 1% to 1.5% so ∆i = 0.005
• P = $1000
• i = 0.01 so 1 + i = 1.01
• The sum of time weighted discounted cash flow is 4901.97:

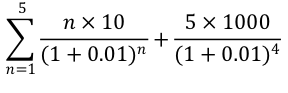
• DUR = 4901.97/1000 = 4.90197 years
• Modified DUR = 4.90197/1.01 = 4.85, that is, a 1 percentage point change in the interest rate leads to a fall in the price of the bond by 4.85%.
• Dollar DUR = -4.90197/1.01 x 1000 = -$4853.46, that is, a 1 percentage point change in the interest rate leads to a fall in the price of the bond by $48.53.

So the price of the security falls by ∆P = -$4853.46 x 0.005 = -$24.27, which represents a 2.4 percent fall in the price of the security, following an increase in the interest rate by 50 basis points. Quite a dramatic fall for such a small change in the interest rate on bonds. For larger changes in the interest rate (derivatives deal with infinitely small changes) and longer maturity (which increase the convexity of the hyperbola linking P and i), a better approximation of the change in the price of a bond can be obtained by calculating the convexity of the bond, which is about the second-order derivative of the price relative to the interest rate.

Thus, if the duration of liabilities and the duration of assets are different, a balance sheet is subject to an interest-rate risk, that is, a rise in interest rate may negatively impact net worth. Some economic units may want to make sure that the price of the securities they hold and the price of the securities they issued are approximately equally sensitive so that net worth does not change significantly with changes in interest rates. Matching the duration of assets and liabilities, or at least mitigating their difference, is an additional concern of financial institutions to matching the liquidity of assets and liabilities and matching the term to maturity of assets and liabilities.

DUR = 4901.97/1000 = 4.90197 years

• Modified DUR = 4.90197/1.01 = 4.85, that is, a 1 percentage point change in the interest rate leads to a fall in the price of the bond by 4.85%.
• Dollar DUR = -4.90197/1.01 x 1000 = -$4853.46, that is, a 1 percentage point change in the interest rate leads to a fall in the price of the bond by $48.53.