Given the recent posts by Daniel Negreiros Conceição and Eric Tymoigne to this blog, and conversations both in the comments section and privately, a revision of my previous post on the topic of modeling the sector financial balances is in order. As before, earlier posts by Rob Parenteau, and Bill Mitchell, in addition to later posts by Daniel and Eric, describe many of the details of this approach and how they fit the graph posted by Paul Krugman. Rob is correct to suggest this would be a much better framework for understanding macroeconomics than the traditional IS-LM model, which was highly flawed to begin. My purpose here is as before is to build on these posts and demonstrate a few uses of the model.First, it must be noted that what we are doing here is merely putting a simple graphical representation to a model that has already been in wide use by many of us for years, and the details for which have been elaborated in much more complex models commonly referred to as “stock-flow consistent models” developed by Wynne Godley, Genarro Zezza, Claudio Dos Santos, Marc Lavoie, and numerous others. Much of this research can be found in publications on the Levy Institute’s website or in the book Monetary Economics: An Integrated Approach to Credit, Money, Income, Production, and Wealth (2006, Palgrave-Macmillan) by Godley and Lavoie. Also, as Eric noted, the SFB model presented here illustrates only financial flows; it is thus showing only a slice of what is presented in the larger models these authors have developed that integrate both flows and stocks coherently and consistently.
As I wrote previously, the sector financial balances model of aggregate demand (hereafter, SFB model) is based upon the following standard macroeconomic accounting identity from any macroeconomics textbook:(1) Private Saving – Investment = (Government Spending – Taxation) + (Exports – Imports)Most neoclassical economists put private saving on the right-hand side of the equation and then multiply by -1, leaving investment equal to private saving, the government surplus, and foreign saving as a result of the trade deficit. This is shown in equation 2:(2) Investment = Private Saving + (Taxation – Government Spending) + (Imports – Exports)
The right-hand side of equation 2 is usually referred to as “national saving” by neoclassical economists, and more “national saving” is thereby thought necessary to increase business investment and thereby increase the economy’s long run capacity to produce goods and services. This interpretation is nearly ubiquitous in the profession.
However, this interpretation (that there is a fixed quantity of something called “national saving,” not the identity itself) is inapplicable except for a fixed exchange rate monetary system operating under a gold-standard or currency-board type of regime in which there is in fact a “fixed” quantity of savings that exists or can be created. But in our flexible-exchange rate monetary system, saving does not finance spending; indeed, the process of loan creation by banks is not reserve constrained, as I have explained in previous posts to this blog.
Those of us employing the framework of J. M. Keynes, Hyman Minsky, Wynne Godley, and others mentioned by Rob and Eric, instead use the above equation to understand changes in the financial status of the various sectors of the economy. That is, instead of saving to finance capital investment (which is not actually what happens), we have “private sector net saving,” which is the addition/subtraction to net financial wealth for the private sector in a given period. If the private sector is net borrowing, then its balance will be negative; if it is net saving, then its balance will be positive.
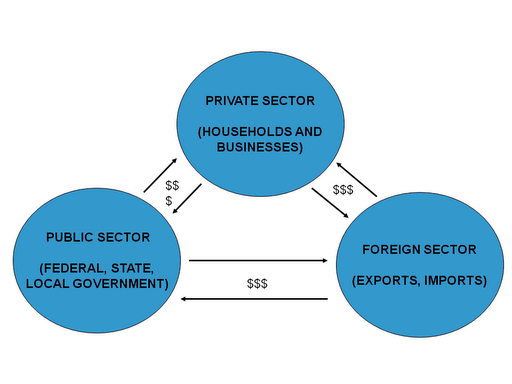
Most importantly, the economy’s financial flows are a closed system, so one sector’s deficit is another’s surplus, and vice versa. There is no way around it, just as it is impossible for every country in the world to have a trade surplus—at least one country must have a trade deficit for the others to have surpluses. Thus, “national saving” as defined in the textbooks (private saving + government surplus + foreign saving) is a misleading concept in our monetary system, since if the government is “saving” some other sector (or combination of them) must not be, by definition. This is represented graphically in Figure 1.
Figure 1: Financial Flows between Sectors of the Economy
For this reason, instead of equation 2, we prefer to write equation 1 as the following:
(3) Private Sector Surplus or Net Saving = Government Deficit + Current Account Balance
The trade balance (exports – imports) is not the precise term to use when considering all financial flows, the current account balance is. For the US, the two very close in magnitude. We’ll call equation 3 the Sector Financial Balances (SFB) equation. Again, this is an accounting identity, not theory. Disagreeing with it is akin to believing the earth is flat. For examples of this framework directly in use on this blog, see here and here.
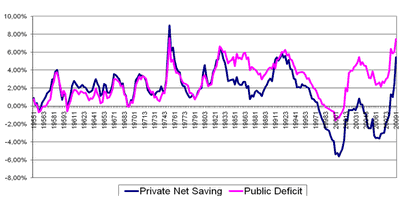
Figure 2 shows how closely the private sector surplus and the government sector deficit have moved historically, which isn’t surprising given they are nearly the opposing sides of an accounting identity. The difference between them, more visible starting in the 1980s, is the current account balance.
Figure 2: Historical Behavior of Private Sector Surplus and Government Sector Deficit as a percent of GDP
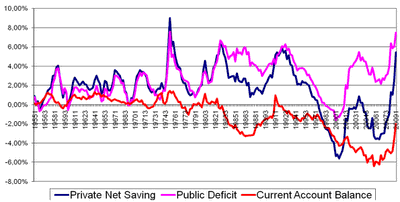
Figure 3 shows all three sector financial balances:
Figure 3: The Sector Financial Balances as a percent of GDP
What we notice from these graphs is that the current rise in the government’s deficit is creating net saving for the private sector. It’s of no surprise to those of us that have been using this framework for years to hear that private saving is rising over the past several months, because we already know that’s usually what an increase in the government deficit does. Of course, the current account balance has also improved, which has also raised the private sector balance.
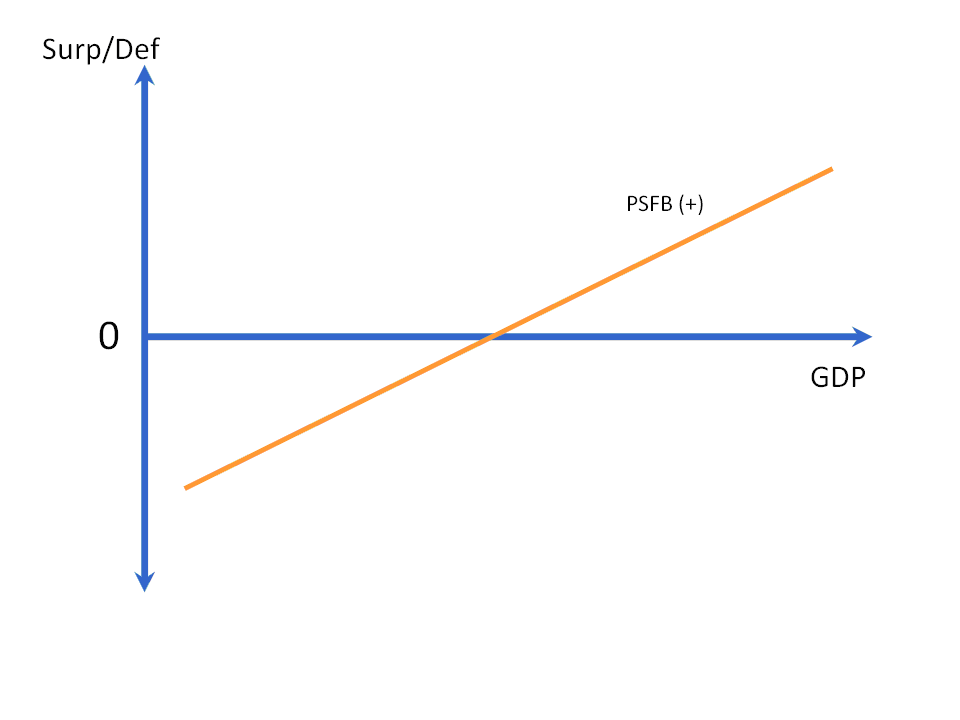
Turning to a graph to represent equation 3, consider first the sector balances individually. First, the private sector financial balance naturally increases with GDP, since higher income means higher net saving, ceteris paribus. As Eric pointed out, because equation 3 is an accounting identity, the sector financial balances are always related as the identity states. That is, there is by definition never a disequilibrium in which one side of the equation is greater than or less than the other. Therefore, graphical representations of a private sector financial balance schedule (hereafter, PSFB) are of desired private net saving relationship to various levels of GDP, while the actual private sector balance will be set by the identity. Figure 4 shows the PSFB(+) schedule.
Figure 4: The PSFB(+) Schedule
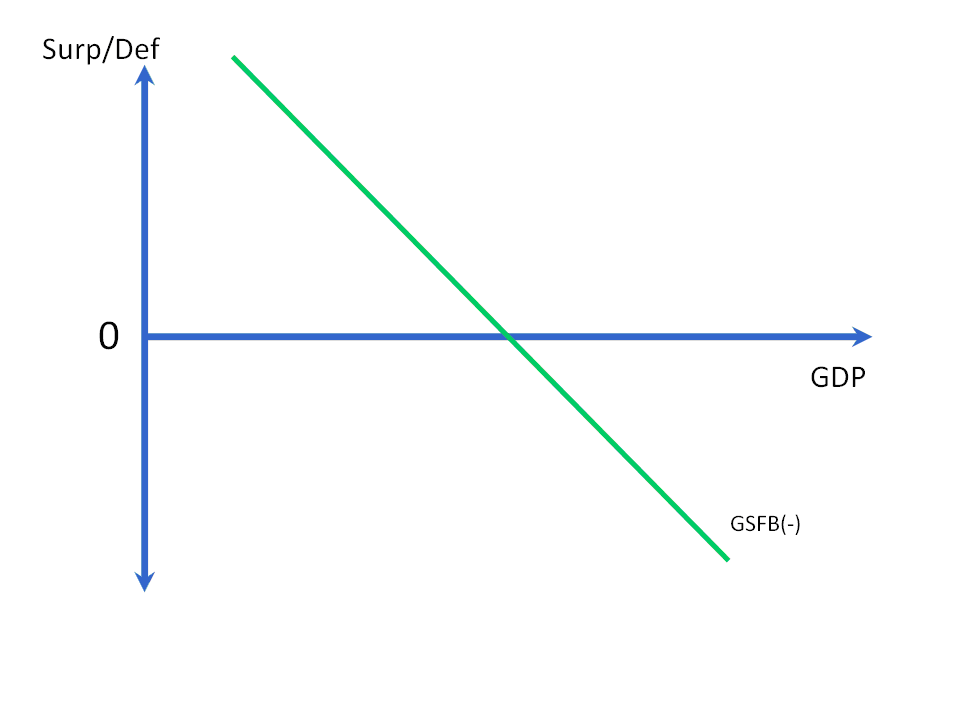
The government’s financial balance will tend to be procyclical as well (that is, higher tax revenues during expansions, and vice versa, etc.). However, because—as shown in Figures 2 and 3—the government’s balance is mostly the opposite of the domestic private sector’s, the graphical representation here of the government sector financial balance schedule (hereafter, GSFB) is of a government deficit schedule (that is, GSFB(-), since points on the schedule below 0 represent government surpluses, and points above it represent government deficits). As Eric pointed out, it is the government sector whose actions enable the non-government sectors together to net save in the domestic currency, while—as Daniel pointed out—the enabling or disenabling of such net saving is a policy variable that one thereby should want to isolate graphically. Figure 5 shows the GSFB(-) schedule depicting the levels of the government sector’s deficits/surpluses as set by existing policies and budgets at various levels of GDP.
Figure 5: The GSFB(-) Schedule
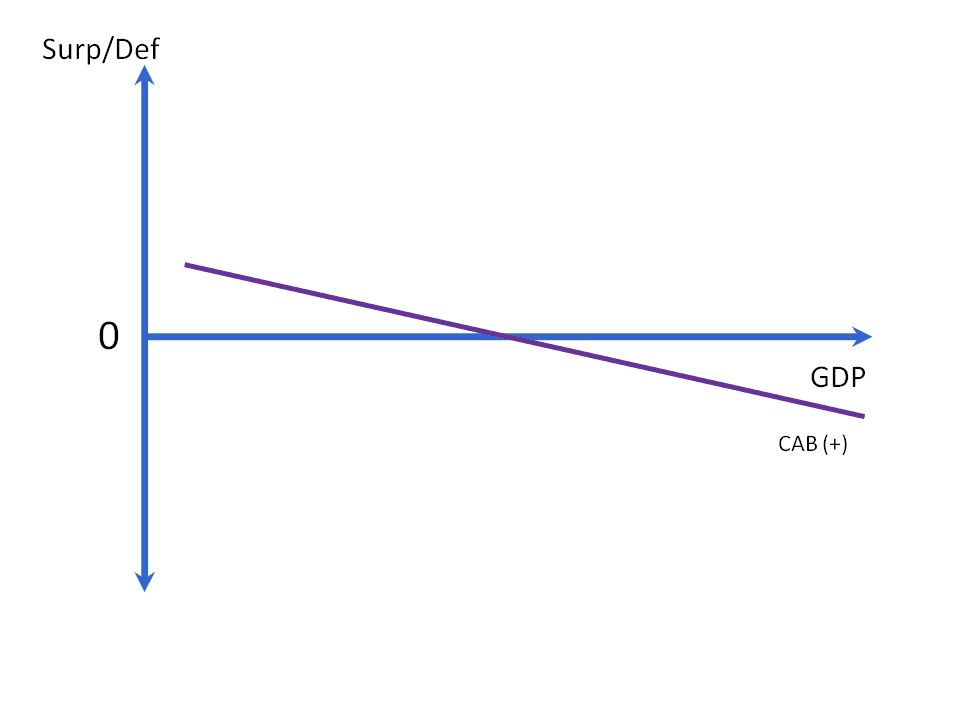
Finally, there is the current account balance, which tends to be countercyclical (that is, as incomes rise, we spend more in imports and the trade balance worsens). Figure 6 shows the desired current account balance (CAB(+)) schedule.
Figure 6: The CAB(+) Schedule
As Daniel, Bill, and Eric have explained, and as I noted above, of particular interest is isolating the government deficit relative to the other balances, as the latter is a policy variable (it seems I was the only one thinking differently by isolating the private sector balance in my earlier post . . . I’ve since come around). As such, the particular version of equation 3 we are after is the following:
(4) Private Sector Surplus – Current Account Balance = Government Deficit
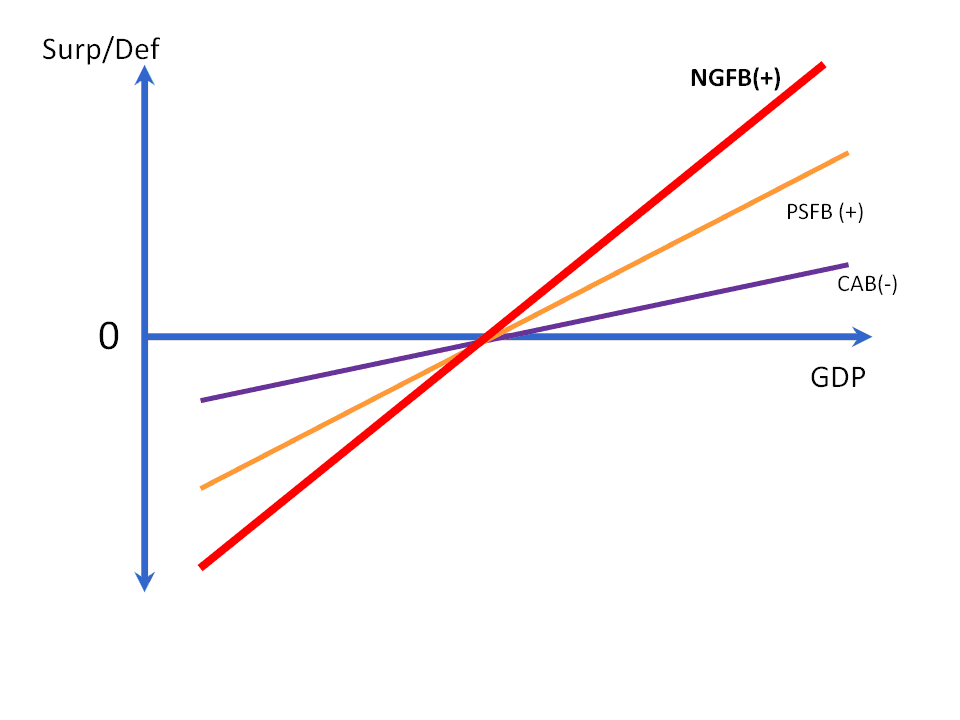
So, what is needed is a schedule combining the elements on the left-hand side of equation 4. Note that the current account balance is subtracted, so now, instead of the CAB(+) schedule, we will have the mirror image of it, the CAB(-) schedule. These together will make up the desired total net saving of the combined non-government sector, represented by the NGFB (+) schedule (for desired non-government financial balance, as Eric labeled it), which is a vertical summing up of the PSFB(+) and the CAB(-) schedules at every level of GDP. This is shown in Figure 7 (the fact that the three lines intersect at a 0 surplus is merely coincidental).
Figure 7: The NGFB(+) Schedule
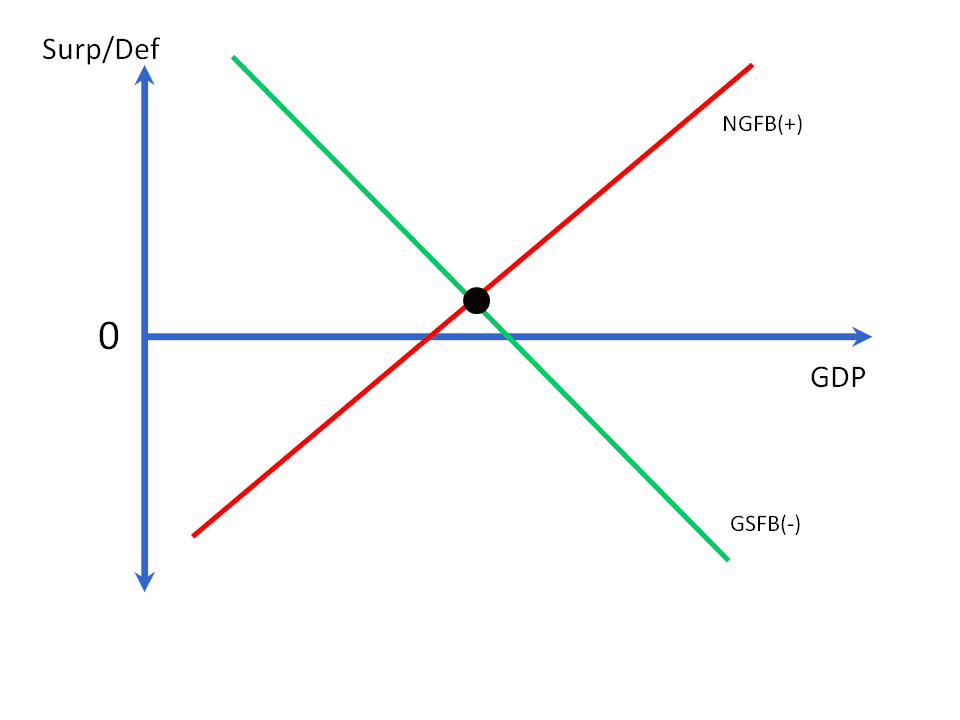
For the SFB model of aggregate demand, we now have the NGFB(+) and GSFB(-) schedules as shown in Figure 8, the intersection of which represents the identity in equation 4.
Figure 8: The SFB Model of Aggregate Demand
Figure 9 shows an application of the SFB model to the late 1990s boom in the US. First, the economy starts the mid-1990s at point A. The financial crises in Asia that weakened those nations’ economies and currencies and thereby substantially lowered the US trade balance shift the CAB(-) line in Figure 7 up (since the CAB(+) shifts down), which shifts the NGFB(+) line up and is represented by the move from point A to point B in the Figure. The effects of previous and then new agreements between Congress and the President to reduce deficits shifts the GSFB(-) line down, represented in the figure as a move from point B to point C. However, instead of GDP falling as a result of these two leakages from aggregate demand, a number of factors including the massive rise in the stock market and “new economy” expectations lead to a historically large increase in the private sector’s willingness to leverage (which continued in the 2000s during the real estate boom after a short recession in 2001-2). This willingness to leverage shifted the PSFB(+) line down markedly, and thus the NGFB(+) line as well, represented by the move from point C to D in the Figure. The overall effect throughout was substantial real GDP growth and lower unemployment. The economy ends the decade at a point like D, with a government budget surplus and current account deficit combining to equal a large negative private sector balance. As shown in Figures 2 and 3 above, for the first time since 1959, the private sector’s financial balance turned negative in 1998, which not coincidentally was the year the federal government ran a budget surplus for the first time since 1969. As the trade deficit increased and the government’s surplus grew through 2000, the private sector’s financial balance grew increasingly negative.
Figure 9: The Economic Expansion of the 1990s
Regarding the current environment, Figures 2 and 3 show a substantial rise in the private sector’s balance as households and businesses have been determined to deleverage after both the 1990s and the further real-estate bubble-induced leveraging of the 2000s. Only the automatic stabilizers prevented a larger decline in GDP. Contributors to this blog (see here, here, and here) have long proposed a fiscal response that directly and quickly raises the private sector financial balance, such as a payroll tax holiday (which restores around $20 billion/week in household and business incomes immediately), immediate block grants to states (which are cutting essential services and raising taxes to balance budgets, as Stephanie Kelton explained), and a jobs program.
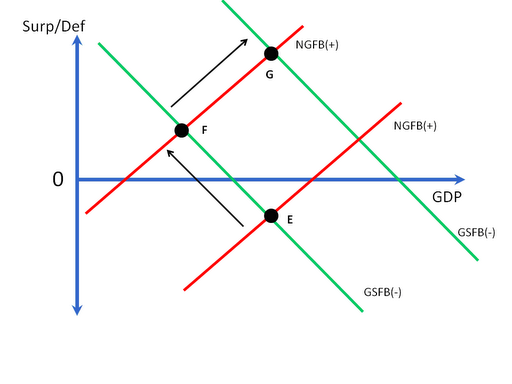
Figure 10 depicts this in the SFB model (Bill Mitchell produced a similar graph and discussion of the model in his post . . . highly recommended as well, with a bit more graphical detail than mine). The net effect of the rise in desired private net saving (shift up of PSFB(+)) and improved trade balance (shift down of CAB(-)) is a shift up in the NGFB(+) line and a move from point E to point F. The economic effect is significantly reduced GDP, while automatic stabilizers and an improvement in the current account balance have raised private net saving (as shown in Figures 2 and 3) and limited the decline in GDP. A well-designed and sufficiently large fiscal stimulus would shift the GSFB(-) line up and move the economy to a point like G, with higher real GDP restored and a still higher private sector financial balance as the private sector attempts to deleverage.
Figure 10: The Current Economic Crisis and the Appropriate Policy Response
The SFB model shows the folly of concerns that households will simply “save” any tax cuts they receive; because the private sector desires to net save right now, if a given stimulus is not enough to quench the need to deleverage and still raise GDP, then the solution is in fact more stimulus to enable the desired deleveraging.
Of course, the recession could also be ended if the NGFB(+) line shifted down to raise real GDP, but that implies an increase in private sector leverage, which is the opposite of what the private sector is currently attempting, or a significant improvement in the current account balance (also not likely given a historically large recession abroad). This explains why using monetary policy—interest rate cuts to encourage borrowing and exports (via depreciation of the exchange rate) which thereby shift the NGFB(+) line—probably won’t work aside from reducing debt service burdens (while it also reduces income for savers, which again decreases the private sector’s financial balance by reducing government interest payments . . . a slight shift down of the GSFB(-) line). Some other ideas popular in economics blogs related to negative nominal interest rates, such as the currency tax—which penalizes those holding transaction balances, and possibly other liquid balances, in an attempt to encourage spending—or the excess reserve tax—which attempts to move short-term, liquid investments into deposits or currency that will then be spent (or so those in support assume)—similarly attempt to raise real GDP by shifting the PSFB(+) and NGFB(+) lines down, and would thus also “work” by reducing the private sector’s financial balance.
In closing, the SFB model of aggregate demand can illustrate rather easily and clearly macroeconomic events and the effects of policies in a manner consistent with actual changes in relative sector financial balances. As Rob explained, it would be a very good replacement for the IS-LM model of aggregate demand. There are many, many other things that can be demonstrated with the model that I don’t have time to go into right now. For instance, the employer of last resort policy proposal is an attempt to make the GSFB(-) line vertical at the full employment level of GDP (which Daniel explained in more detail); or, as another example, the SFB model shows that aggregate demand is set by the government’s deficit relative to net savings desires of the non-government sectors (as Warren Mosler says, the government’s deficit is the “M” in the quantity theory of money (MV=PY), while the desired leverage of the non-government sector (the opposite of its desire to save) is the “V” in the equation).













10 responses to “The Sector Financial Balances Model of Aggregate Demand—Revised”