Why Money Matters

By L. Randall Wray*

Our Mission Oriented Finance conference explores how to direct funding toward what Hyman Minsky called “the capital development of the economy”, broadly defined to include private investment, public infrastructure, and human development. (See more here.)

But to understand how, we need to understand what money is and why it matters. After all, finance is the process of getting money into the hands of those who will spend it.

The dominant narrative is that money “greases” the wheels of commerce. Sure, you could run the commercial machine without money, but it runs better with lubricant.

In that story, money was created as a medium of exchange: instead of trading your banana for her fish, you agree to use cowry shells to intermediate trade. Over time, money’s evolution increased efficiency by selecting in succession unworked precious metals, stamped precious metal coins, precious metal-backed paper money, and, finally, fiat money comprised of base metal coins, paper notes, and electronic entries.

However, that never changed the nature of money, which facilitates trade in goods and services. As Milton Friedman famously proclaimed, in spite of the complexity of our modern economy, all of the important economic processes are revealed in the simple Robinson Crusoe barter-based economy.

Money is a “veil” that obscures the simple reality; in the conventional lexicon, money can be ignored as “neutral”. (For those well-versed in economics, we need only refer to the Modigliani-Miller theorem and the efficient markets hypothesis that proved finance doesn’t matter.)

We only worry about money when there’s too much of it: Friedman’s other famous claim is that “inflation is always and everywhere a monetary phenomenon”—too much money causes prices to rise. Hence, all the worry about the Fed’s Quantitative Easing, which has quadrupled the “Fed money” (reserves) and by all rights should be causing massive inflation.

This post will provide a different narrative, drawing on Joseph Schumpeter’s notion that the banker is the ephor of capitalism.

Looking at money from the perspective of exchange is highly misleading for understanding capitalism.

In the Robinson Crusoe story, I’ve got a banana and you’ve got a fish. But how did we get them? In the real world, bananas and fish have to be produced—production that has to be financed.

Production begins with money to purchase inputs, which creates monetary income used to buy outputs.

As mom insisted, “money doesn’t grow on trees”. How did producers get money in the first place? Maybe by selling output? Logically, that is an infinite regress argument—a chicken and egg problem. The first dollar spent (by producer or consumer) had to come from somewhere.

There’s another problem. Even if we could imagine that humanity inherited “manna from heaven” to get the monetary economy going—say, an initial endowment of a million dollars—how do we explain profits, interest, and growth?

If I’m a producer who inherited $1000 of manna, spending it on inputs, I’m not going to be happy if sales are only $1000. I want a return—maybe 20%, so I need  $1200. If I’m a money lender, I lend $1000 but want $1200, too. And all of us want a growing pie. How can that initial million manna do double and triple duty?

Here’s where Schumpeter’s “ephor” comes in. An ephor is “one who oversees”, and Schumpeter applied this term to the banker. We do not need to imagine money as manna, but rather as the creation of purchasing power controlled by the banker.

A producer wanting to hire resources submits a prospectus to the banker. While the banker looks at past performance as well as wealth pledged as collateral, most important is the likelihood that the producer’s prospects are good–called “underwriting”. If so, the ephor advances a loan.

More technically, the banker accepts the IOU of the producer and makes payments to resource suppliers (including labor) by crediting their deposit accounts. The producer’s IOU is the banker’s asset; the bank’s deposits are its liabilities but are the assets of the deposit holders (resource suppliers).

This is how “money” really gets into the economy—not via manna from heaven nor Friedman’s “helicopter drops” by central bankers.

When depositors spend (perhaps on consumption goods, perhaps to purchase inputs for their own production processes), their accounts are debited, and the accounts of recipients are credited.

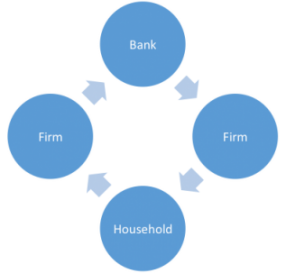Today, most “money” consists of keystroked electronic entries on bank balance sheets.

Because we live in a many bank environment, payments often involve at least two banks. Banks clear accounts by debiting claims against one another; or by using deposits in correspondent banks. However, net clearing among banks is usually done on the central bank’s balance sheet.

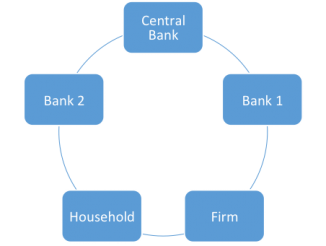
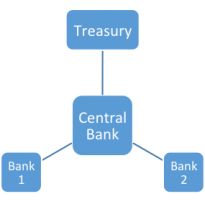
Like any banker, the Fed or the Bank of England “keystrokes” money into existence. Central bank money takes the form of reserves or notes, created to make payments for customers (banks or the national treasury) or to make purchases for its own account (treasury securities or mortgage backed securities).

Bank and central bank money creation is limited by rules of thumb, underwriting standards, capital ratios and other imposed constraints. After abandoning the gold standard, there are no physical limits to money creation. We cannot run out of keystroke entries on bank balance sheets

This recognition is fundamental to issues surrounding finance. It is also scary.

The good thing about Schumpeter’s ephor is that sufficient finance can always be supplied to fully utilize all available resources to support the capital development of the economy. We can keystroke our way to full employment.

The bad thing about Schumpeter’s ephor is that we can create more funding than we can reasonably use. Further, our ephors might make bad choices about which activities ought to get keystroked finance.

It is difficult to find examples of excessive money creation to finance productive uses. Rather, the main problem is that much or even most finance created to fuel asset price bubbles. And that includes finance created both by our private banking ephors and our central banking ephors.

The biggest challenge facing us today is not the lack of finance, but rather how to push finance to promote both the private and the public interest—through the capital development of our country.

That is the main topic of our Mission Oriented Finance conference.

*Cross posted from FT’s Alphaville