By Paul Meli
There are many important laws that determine the behavior of various systems within the Universe but as far as economics is concerned, none is more important than the concept of a closed system.
From Wikipedia:
”In non-relativistic classical mechanics, a closed system is a physical system which doesn’t exchange any matter with its surroundings, and isn’t subject to any force whose source is external to the system. A closed system in the classical mechanics sense would be considered an isolated system in thermodynamics.”
What does this mean in the context of a monetary economy? What could properties of a physical system have in common with a system based largely on the relationships between stocks and the flows between them? It turns out that some math systems behave according to the same rules that constrain elemental physical particles, i.e. the concept of the conservation of matter holds mathematically for the “conservation” of currency units within the system.
If we define the closed system as the universe of state-backed US dollar assets and liabilities, including state-issued bonds held by the public, it means that the net dollar assets existing in the economic system cannot change over some period of time t without an add or subtract from a source external to the system.
The graphic below illustrates a circuit composed of a collection of closed systems within the (I-S) component of the sectoral balances identity. It is defined to highlight net flows between selected groups within the domestic non-government under certain assumptions. The arrows represent the net flows. Flows move in both directions but only net flows are illustrated. Flows are measured over some time period t, usually a year. The circuit as defined accounts for the bulk of transactions that occur within the economy important to the financial well-being of the majority of participants.
The model is based on the following assumptions:
- Businesses are able to earn a profit in the aggregate (p>0).
- Net exports is assumed to be zero.
- Net government spending is initially zero.
Let x = total business investment spending over period t.
p = net profit over the period as the difference between Sales and Investment.
i = interest on household debt accrued in the system over the period.
(x+p) = total sales revenue collected by businesses over the period.
The assumptions and assignments above are the most conservative possible, any real-world conditions would increase the requirement of net government spending.
Observations:
If (G-T)=0, p>0 is a closed system violation (which is impossible). Business entities are attempting to create net flow between some level of investment (x) and some level of sales revenue (x+p). Since households contain only x after the investment not accounting for net savings, which would require prior net (G-T > 0), it is only possible for business entities to extract x in sales. Thus, p>0 is only possible if (G-T) > 0 or the funds required are obtained through the issuance of private debt.
There is a point of view that an economy can operate in a steady state on private debt alone without deficit spending. Let’s take a look.
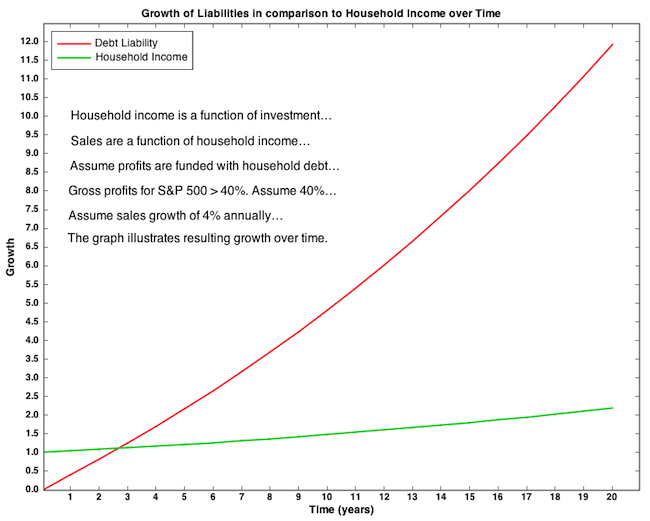
Why do the liabilities accrue so fast? For one thing, no amount of borrowing can eliminate the liabilities previously existing. This is a consequence of the nature of debt – it is “money” issued as an asset with an equal offsetting liability that nets to zero on individual balance sheets and on all balance sheets in the aggregate. Increasing debt merely adds to the balance accruing interest. The graph illustrates growth in the principal portion only, not including interest, which would make matters worse (and the computation more complicated).
Households ultimately pay for all principal and accrued interest from private debt in the system, either directly as a result of consumer debt or indirectly as a result of business debt costs having been rolled into the price of products they consume.
The purpose of this exercise was to demonstrate that no series of transactions within a closed system is capable of generating net nominal growth, even through ever-expanding debt. Nominal growth can only occur as a result of net government spending.
This is presented as a general argument, and is not intended to be a rigorous mathematical proof, which it is not. It is an attempt to illustrate the general relationships between the main sector flows within the domestic economy…which is a closed system.
Paul’s excellent illustration provides an insight to a very valid concept that hasn’t been well understood.With the world wallowing in ‘debt’ and all the political gangster crying austerity, it’s time people woke up to the way the monetary system really works. Austerity is just plain stupid in the depths of a recession as is the concept of a balanced budget at the macroeconomic level. If the Government doesn’t spend there is no money flowing into the private sector. Because the private banks gradually soak up the existing money supply, through being allowed to charge compound interest on the loans they make, there has to be a flow of new money into the system just to keep the system alive.
I know most of the readers don’t need this, but … since you began with a Scientific reference, perhaps you could follow the rules for a well-written Scientific article, all variables are defined before they appear in an equation or figure.
Questions? I thought I had everything defined that needed to be, but I’m open to suggestions.
Yes, that would help. Start with I-S. Is it Investment (hyphen) Savings? Or Investment (minus) Savings? Or do the I and the S stand for something else?
YES John! People use dashes and slashes all the time to mean god-knows-what, usually (I think) NOT subtraction and division. Drives me nuts.
Sorry guys, my mistake. I assumed everyone that might be intersted in this would be familiar with the sectoral balances identity.
The identity:
(G-T) + (I-S) + (X-M) = 0; where
G = Federal government spending
T = Federal income taxes
I = Private investment (Business, not financial)
S = Private savings
X = Exports
M = Imports
(G-T) = Net government spending, positive if in deficit, negative if in surplus.
(I-S) = Net private savings, positive if in deficit, negative if in surplus.
(X-M) = Net exports, negative if in deficit, positive if in surplus.
This equation must always be true by definition, it is an identity.
Professor Bill Mitchell goes through the derivation of this identity in nearly every one of his blogs and Saturday quizzes. He repeats it endlessly because it forms the basis of MMT thinking. I reccommend you re-read it every chance you get if you wish to understand MMT.
Paul, a lot of we non-economists pass these articles along to our family members, and need these things explained every single time otherwise their eyes glaze over. I don’t think you realize how important these posts are to breaking through the fog.
Thx
P.S. Don’t ever be embarrassed about being too plain speaking, either. Readers appreciate it.
MRW,
I too am a non-economist. My degree is in mechanical engineering, my experience is spread over real-estate appraising, a stint (20 years) as a general contractor and finally over the last decade+ as a structural engineer…finally got to use my education directly.
This is different from the sectoral balance equations I have seen before. I’m having a hard time grasping the significance of I-S as representing the private non-government deficit or surplus. Usually it’s referred to as private sector savings, meaning the portion of private sector income that is not spent. That would be S, I think. I can’t imagine what you get if you subtract that from business spending, which you have defined one way in your article and differently in your response below. In the article, it is all spending (net profit plus I = Sales) and later you identify elements of I that include only cost of goods sold, not other expenses that are subtracted to find net profits. Which version of I is used in sectoral balances, and why not just take total private (household and business) savings? Why the subtraction?
Then there is a mention on the graph that S&P 500 gross profits are 40% of sales. Gross profit is mentioned only in the graph, otherwise you talk of net profit. I think net profit must be what you want to use in calculating the graph, and it is much closer to 5% of sales, I think.
And I’m getting a hint that by “businesses” in the economy, you include only publicly traded companies, not closely-held corporations, or unincorporated small businesses, which look a lot like households, with respect to this area of macroeconomics.
Net profits is also not the portion of sales that does not flow back to households. Dividends and stock buybacks also flow to households, and are included in net profits. Ultimately, all profits flow to the owners of the business, unless you are to assume that retained earnings increase without limit. Typically, when a new business matures, its level of retained earnings tends to stabilize, and it returns its profits to the owners in the form of dividends.
Checkmate Paul!
“This is different from the sectoral balance equations I have seen before. I’m having a hard time grasping the significance of I-S as representing the private non-government deficit or surplus.”
Sorry, but I can’t help you here. The article assumes some familiarity with the sectoral balances. I have however, in the responses to others in the thread, addressed most of your questions.
“net profit”
Sorry, the line that reads: “p = net profit over the period as the difference between Sales and Investment.”
should be: “p = GROSS profit over the period as the difference between Sales and Investment.”
I hope you aren’t conflating the S in the term sales with S in the sectoral balances, which refers to Saving. That would be a fatal error in terms of understanding the material.
There is virtually no economic significance to gross profit, as the term is commonly used in accounting.
The income statement looks something like
Sales…………………………100
Cost of Goods Sold
Direct labor…………40
Raw materials………20
(other)………………..5
Gross profit………………….35
Expenses
Rent……………………5
Taxes………………….5
Depreciation………..10
Travel and Entertainment …5
Other expenses…….4
Net Profit …………………………..6
Sorry all the columns don’t align, but you get the idea.
Nowhere in the income statement is anything for current spending on capital goods, which in accounting is known as “investment” The cost of capital goods is spread over their lifetime and accounted for as a depreciation expense.
As has been noted, if you want to use these same words to have other meanings, you must say so in advance. Otherwise it’s Alice in Wonderland for anyone trying to understand you, when words mean whatever you want them to mean at the time.
“Nowhere in the income statement is anything for current spending on capital goods, which in accounting is known as “investment” The cost of capital goods is spread over their lifetime and accounted for as a depreciation expense.”
I stated what”Investment” included elsewhere in the comments (see 1/1/2012 6:38 AM). It doesn’t matter what I call it, Profit = Revenue (sales) – Expenses (investment as booked and allocated by accountants). That’s all there is folks. Eventually, every cost of business one way or the other comes home to roost and subtracts from revenue. That’s the power of aggregates. One can quibble over definitions, or whatever, but it doesn’t have diddly to do with the final arithmetic, which is what this post is about.
You’ve missed the forest for the trees.
The cost of each and every one of those capital goods (or it’s depreciated allocation) subtracts from revenue within the period and the company reports a profit/(loss). No dollars disappear. They are conserved. A companys inflow minus it’s outgo over the period as it is booked (is that simple enough?) determines whether it has earned a profit/(loss) over the period. A billion transactions in between doesn’t give us any extra information that is useful to anyone other than accountants, and nothing is created out of thin air. Only the government can do that.
By analyzing the aggregate, all of that noise is eliminated.
If you have to bring out individual hypothetical balance sheets to prove your argument you’re already losing. There are literally billions of transactions that take place every cycle. Good luck with that. Get back to me when you’ve weeded through them.
BTW. the average gross profit reported by S&P 500 companies is over 40%. That tells us much more than your made-up income statement.
PAUL:
The fact that some money ends up as profit (or rent or wages or interest for that matter) does not mean it is forever out of the spending stream. If the money is spent back into the spending stream, everything is fine. The problem arises when the money is LENT back into the spending stream, because this means the money IS forever out of the spending stream, and likely the interest paid will be out, as well. The problem, I think, is not so much “profit” as “interest”.
But anyway, good post.
Art
I’m afraid I still find this confusing. You introduce a number of other quantities which don’t correspond to what I remember from economics classes, then add a confusing diagram .
You define net profit as “the between Sales and Investment”. I thought profit was revenue minus costs, while “investment” is money put into business assets, R&D, etc. I’ve never heard of the cost of goods sold being termed “investment”.
The diagram gives a few net flows to a few entities. If the arrows show the net flows, then you seem to be stating that wages come from government spending (the only arrow into the “households” circle) and nothing ever leaves banks (perhaps to be expected given the tenor of this blog). You also seem to make the same mistake that Marxists make, assuming that profits disappear from the economy (though I’ve never found a case of profits stored under the corporate mattress). Profits are put back into the business (e.g. spent on plant and equipment), returned as dividends, or kept in a bank or investment (which then uses the money). They don’t disappear from the economy.
So I guess I’d need a better introduction to your economic system (since it doesn’t match any I’m familiar with), as written it makes no sense.
“Since households contain only x after the investment not accounting for net savings, which would require prior net (G-T > 0), it is only possible for business entities to extract x in sales”
There is a problem here that you may have overlooked. ‘x’ is a stock.
Once ‘x’ is in injected into the system it can flow round many times before the capital item ‘x’ bought wears out.
That is the concept of ‘stock turn’ or ‘turnover’ – which is a flow and will be many many times ‘x’ over the lifetime of the capital asset. ‘p’ is extracted from this flow.
You have to add a time element to your model. ‘x’ is injected and then it is extracted and reinjected. Similarly the ‘p’ that is extracted is used to purchase goods and services for the business owners, pay interest and principal
Each extraction cycle is (x-p) + p – which represents the split of each turn between labour and capital.
Steve Keen has already done the work to show that the private circuit can be stable on its own if everything is recycled at the correct rate. Why are we still pushing the myth that it can’t be?
“Steve Keen has already done the work to show that the private circuit can be stable on its own if everything is recycled at the correct rate, Why are we still pushing the myth that it can’t be?”
Neil, don’t take it personally, and pardon me if I don’t just take your word for it.
“if everything is recycled at the correct rate”
This is the kicker, I don’t see how that can be accomplished within a closed system. But I am all eyes. I’m willing to look at his/your argument. It may turn out that we don’t actually disagree, we’re just stating the outcomes in different terms.
Rather than argue from a position of someone else’s authority, why don’t you present the argument in your own words since you seem so sure I’m wrong. I can always learn something new and I don’t wish to be the purveyor of mis-information. I do have the reality of recent events to support my position however. How does Keen explain that?
“The fact that some money ends up as profit (or rent or wages or interest for that matter) does not mean it is forever out of the spending stream. If the money is spent back into the spending stream, everything is fine.”
Art, a couple of things…
Companies don’t reinvest profits completely back into the economy, that’s why we have companies siiting on some $2 Trillion in cash now. Second, I’m not sure it would be possible for companies to reinvest “excess” profits back into the economy because there would likely not be enough sales…they would end up increasing inventory.
There’s a reason companies aren’t “creating jobs” right now. They don’t actually create jobs, they extract funds from households when households have them.
ThomasW,
+1
See my comments here: http://mikenormaneconomics.blogspot.in/2012/10/paul-meli-sectoral-balances-within.html
“I’m afraid I still find this confusing. You introduce a number of other quantities which don’t correspond to what I remember from economics classes, then add a confusing diagram.”
Thomas, sorry about the confusion, the diagram is intended to clarify and simplify. Also, it is not presented as “economics”, which in it’s current mainstream form is little more than political advocacy.
This is a math exercise intended to show the way in which flows move through the economy under certain assumptions.
” I thought profit was revenue minus costs, while “investment” is money put into business assets, R&D, etc. I’ve never heard of the cost of goods sold being termed “investment”.”
Investment is spending on plant, equipment, labor, materials and financing. These are “costs” of production. If the investment doesn’t return more than was spent, it isn’t much of an investment from a business point of view. Investment on public purpose is another story.
“…If the arrows show the net flows, then you seem to be stating that wages come from government spending (the only arrow into the “households” circle)…
I’m demonstrating (trying) that funds for growth, and the funds necessary for companies to realize profits, must come from net government spending. There is no other source possible. If those funds enter the economy through workers, the unemployed and transfer payments, unemployment is reduced.
As an aside, I will take this opportunity to point out an economic reality. It is impossible for businesses in the aggregate to succeed on sales to their own employees. Their success is dependent upon two things the government provides…direct hiring of part of the workforce and direct purchase of goods and services from private businesses.
So much for the idea of a “libertarian paradise”.
…and nothing ever leaves banks (perhaps to be expected given the tenor of this blog).”
In the net, nothing does ever leave banks. More accumulation of financial assets.
“You also seem to make the same mistake that Marxists make, assuming that profits disappear from the economy (though I’ve never found a case of profits stored under the corporate mattress).
What are Retained Earnings? Reports have the total in the $2 Trillion range.
Profits are put back into the business (e.g. spent on plant and equipment)…
Not all profits, hence Retained Earnings.
“…or kept in a bank or investment (which then uses the money)…”
Banks don’t “use” deposits except as a metric to allow them to expand debt. The money banks lend is issued from “thin air”.
“…They don’t disappear from the economy…”
Might as well. Accumulation of financial assets is the functional equivalent of “warehousing” of excess inventory (cash).
Every definition I’ve seen of “investment” is essentially plant and equipment. In the MMT sector balances equation, (S-I) refers to investment defined as plant and equipment. To define investment as all business costs is to define a re-define the term and then use both the new definition and the old one (when you give S-I) without specifying which is being used. I notice in your comment on the link Ramanan listed above that you state this is your own definition of investment. If you’re trying to treat economics like a science or mathematically you need to define your terms before using them. It’s also traditional to use commonly accepted terms rather than inventing new ones, and especially not redefine a term with a common meaning.
I also don’t understand the statement that businesses cannot succeed on sales to their own employees. I never said that, I don’t know of any economist who says that. If I were to guess, you’re defining “business” to mean all of the private sector and “own employees” to mean all workers in the economy, as this is consistent with the MMT message of prosperity through government deficits, which you appear to be trying to argue.
What does a “libertarian paradise” have to do with anything?
As to Retained Earnings, a bunch of retained earnings are overseas – companies are avoiding taxes by leaving any money possible outside the United States. Other retained earnings are in banks or short term investments. Banks are certainly sitting on a huge amount of money ($2 trillion in reserves as opposed to $40 billion prior to 2008), the Fed is now paying them interest on that money. I can, however, assure you that after 35 years in private industry I have NEVER seen a company keep a room full of cash sitting idle.
Given the fact you haven’t defined your terms, use multiple definitions for at least one term, and are trying to argue from some poorly labeled, extremely incomplete diagrams, I can’t see any evidence that you’ve demonstrated anything here.
“Every definition I’ve seen of “investment” is essentially plant and equipment.” – Thomas W
You have apparently missed a lot.
Investment = Plant, equipment, materials, labor, financing costs and other expenses involved in the cost of bringing a product to market.
Every business has expenses, however you categorize them, and the inflow must be greater than the outflow in order for them to realize a profit. This is not rocket science, yet somehow you have missed the forest for the trees.
Rather than focus on your misunderstandings of the very definitions you are criticizing me for getting wrong, and of simple mathematical relationships, which just becomes a he-said-she-said anyway, let me pose a simple question:
If a business doesn’t recoup all of the costs, expenses, etc. that are incurred through it’s operations, how is it possible that it would even break even, let alone make a profit? Or do you believe that negative profits (losses) are a good outcome?
The expression for this relationship is Revenue (sales) minus Investment (expenses) = gross profit. Look it up. This is the bottom-line of transactions between households and business entities.
The rest of your criticisms have no target, you will have to express yourself more clearly to get a response.
I understand the basic concepts of business accounting. Profit is broadly revenues minus costs. Businesses where revenues are lower than costs lose money. I don’t see any connection with government deficits.
I also think I need to know the definition of savings (S in your sector balance equation). I can’t see any way (S-I) can ever be positive with investment (I) being all plant, equipment, materials, labor, financing costs and other expenses.
Good point. Normally, Savings means the portion of private sector income that is not spent, and it is the addition to private sector net financial assets. Which is itself the relevant quantity for the sectoral balance equation, without reference to I or any other quantity, however defined.
I do see, though, how one might want to subtract business capital spending from all private sector savings in order to get the relevant number for sectoral balances, if one were to calculate S as the sum of household savings and business profits plus depreciation. In that case business investment spending would have been counted both in spending and in savings, so I (= business investment spending not on the income statement) would have to be subtracted out in order to avoid double counting it.
Neil,
“There is a problem here that you may have overlooked. ‘x’ is a stock.”
x is both a stock and a flow, depending on when you examine it. It’s a flow when the business spends (invests) it. It adds to the stock of funds in the household sector. Funds are always a stock except for the instant in time when a transaction occurs, if we want to get technical.
“Once ‘x’ is in injected into the system it can flow round many times before the capital item ‘x’ bought wears out. That is the concept of ‘stock turn’ or ‘turnover’ – which is a flow and will be many many times ‘x’ over the lifetime of the capital asset. ‘p’ is extracted from this flow.””
Right, it flows around many times but the “stock” doesn’t get any bigger. As it circulates, it merely adds to the running total of GDP, which is a number unrelated (in the closed system sense) to the stock of funds existing in the economy. An increase in GDP has zero effect on the stock of funds.
Along the way, little bits of profit are extracted until x decays to nothing among households (except for saving). Businesses however now hold x+p. (If the government follows through with the appropriate deficit spending ).
A net transfer of funds from a finite stock to another sector, one which doesn’t (can’t) return the favor without philanthropy or going out of business.
Question of sectoral balances within a private sector becomes more perplexing once you consider tangible assets as well as financial assets. Households and companies can investe in tangible assets whose value (partially?) can compensate for increased indebtedness. This supports whole increasing private debt structure and the problem is not so much profit that companies make, after all, they pay them back to the households as dividends.
Companies run some sort of ‘buffer-stock’ of financial assets but even desire for larger buffer stock will get saturated eventually, and then the households will get the money. Much bigger problem are saving desires arising from demographics because demand for financial assets arising from pension saving of the aging population can become quite overwhelming if we continue to pretend that governments are like households.
This is not an invalid thing to think about, it is simply presented sloppily.
There is nothing wrong with dividing the sectors further for more granular analysis. You can divide the domestic private sector into households and businesses and analyze the flows between them. Clearly if the businesses are accumulating financial assets, and the system is closed, then households must be depleting them. You can divide them into “the 1%” and “the 99%” and analyze the flows between them as well, and that is being done a lot on this blog, perhaps even less rigorously than was done here.
Real assets are another thing entirely. Real assets can be created and grow because of labor inputs, and that, in the end, is how a society becomes more prosperous. It is not impossible to have households dissaving in the aggregate, for a short time, if they are taking loans to make large purchases simply to spread the cost over the life of the asset. It’s just not sustainable forever.
The good news about demographics is that the baby boomers are now changing from big savers to big dissavers, as they retire. That will lessen the need for inputs of financial assets from outside the domestic private sector.
I was thinking about the process where, for example, household takes out a loan to build a new house and loan creates financial assets and liabilities that both net to zero, but the newly build house has market value that does not have offsetting liability.
Say household takes out a loan worth 100k and build a house that has market value of 100k, then net worth of the household has not changed, new assets equal new liabilities. Only looking at the financial assets though, household is 100k down and so someone else in the economy holds new financial assets worth 100k. I think this process could explain behaviour of the private sector to the large extent and general tendency of private debt levels to rise.
Yes, the $100K financial assets went to the contractor who built the house, and his employees, and his suppliers.
There is a general tendency for everything to increase, because of the trend of increase in population, productivity, and real wealth. Overlaid on that are cyclical increases and decreases (think housing bubble). A general trend of increasing household debt relative to household income or wealth would be unsustainable, as debt servicing ability is dependent on wealth and income.
“This is not an invalid thing to think about, it is simply presented sloppily.” – Golfer John
Really? Sloppy in what way? The arithmetic couldn’t be any simpler, as it only requires addition and subtraction, and it’s accounting consistent. I put more effort into this than you did your criticism. Why don’t you make a less content-free criticism and be specific? I don’t mind honest criticism, in fact I encourage it.
“a private sector becomes more perplexing once you consider tangible assets as well as financial assets.”
Guys, we’re tracking NOMINAL FINANCIAL ASSETS with the sectoral balances, which is all the S/B accounts for. There are no “real” assets anywhere to be found anywhere in my presentation or in the sectoral balances identity, nor are they relevant to the discussion.
The various arguments presented by Thomas W, John O’Connel and now Golfer John are all straying away from the central argument. Net dollar-denominated financial assets backed by the state are conserved. No combination of economic activity can add to or decrease the amounts. It is axiomatic and easily proved.
It is a demonstration of the “conservation of dollar-denominated financial assets backed by the government”.
All of your arguments distill down to this: You are claiming that real growth can grow relative to nominal growth without limit. Unlimited leverage. Companies can’t extract profits in the form of real assets. Show me the money. I have never seen a Profit and Loss statement where a business entity reported it’s earnings in widgets.
Businesses don’t remove “phantom” profits from the system, and any dollar gains after accounting for liabilities in the aggregate have to come from somewhere. The gains are accounted for on balance sheets as cash and gains can only come from one possible source. Want to guess where?
The point you want to make might be better made with reference to cash flow rather than income. But then, you don’t know the difference, do you?
And Paul, no one can pay their taxes in real assets… rsp